题目内容
【题目】如图，矩形BCDE的各边分别平等于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后第2015次相遇地点的坐标是（ ）
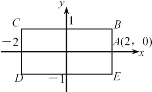
A. （2，0）B. （－1，－1）C. （－2，1）D. （－1，1）
【答案】B
【解析】
利用行程问题中的相遇问题，由于矩形的边长为4和2，物体乙是物体甲的速度的2倍，求得每一次相遇的地点，找出规律即可解答．
矩形的边长为4和2，因为物体乙是物体甲的速度的2倍，时间相同，物体甲与物体乙的路程比为1:2，由题意知：
第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×
=4,物体乙行的路程为12×
=8，在BC边相遇；
②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16，在DE边相遇；
③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×=12,物体乙行的路程为12×3× =24，在A点相遇；
此时甲乙回到原出发点，则每相遇三次，两点回到出发点，
∵2015÷3=671…2，
故两个物体运动后的第2015次相遇地点的是：第二次相遇地点，
即物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16，在DE边相遇；
此时相遇点的坐标为：(1,1).
故选B.
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
【题目】“母亲节”快到了，七（1）班班委发起慰问烈士家属王大妈和李大妈的活动，决定在“母亲节”期间全班同学利用课余时间去卖鲜花筹集资金．已知同学们从花店按每枝1.4元买进鲜花，并按每枝3元卖出，设卖出鲜花x枝．
品名 | 热水壶 | 电饭煲 |
单价(单位：元/只) | 125 | 250 |
（1）每卖出一枝鲜花赚_______元，卖出鲜花x枝赚______元；
（2）若从花店购买鲜花的同时，同学们还花了50元购买包装材料，请把所筹集的资金y（元）用鲜花的销售量x（枝）的代数式表示；现在筹集的资金为750元，问需要卖出鲜花多少枝？
（3）已知两种家用小电器的单价如下表所示，现将筹集的750元全部用于购买表中家用小电器赠送两位大妈，且电饭煲至少要购买1只，请求出所有的购买方案.
