Question

【题目】如图，在四边形ABCD中，对角线AC、BD交于点E，点E为BD的中点，∠BAC+∠BDC=180°，AB=CD=5，tan∠ACB=，则AD=______ ．

Answer 1

【答案】2

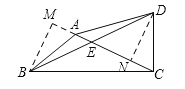
【解析】解：过B作BM⊥CA，交CA的延长线于M，过D作DN⊥CA，垂足为N，∴∠BME=∠DNC=90°．∵点E为BD的中点，∴BE=DE．∵∠BEM=∠DEN，∴△BME≌△DNE，∴BM=DN．∵AB=CD，∴Rt△ABM≌Rt△DCN，∴∠BAM=∠DCN．∵∠BAC+∠BDC=180°，∠BAC+∠BAM=180°，∴∠BDC=∠BAM，∴∠BDC=∠DCN，∴DE=CE，∴BE=CE=DE，∴∠DBC=∠ECB，∴∠DBC+∠BDC=∠ECB+∠DCN，∴△BCD是直角三角形．∵tan∠ACB=，∴tan∠DBC=．∵DC=5，∴BC=10，在△BMC中，设BM=x，则CM=2x，由勾股定理得：x2+（2x）2=102，x=±，∴BM=DN=，CM=，由勾股定理得：AM= ==，∴CN=AM=，∴AN=CM﹣AM﹣CN=﹣﹣=，在△ADN中，AD====．故答案为：．