Question

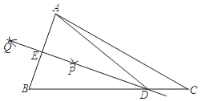
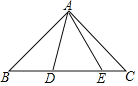
【题目】如图1，AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线，过点A作AE⊥AD，交BD的延长线于点E.

（1）求证：∠E=∠C；

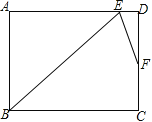
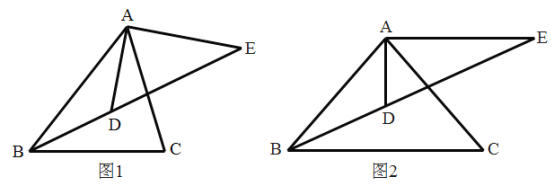
（2）如图2，如果AE=AB，且BD：DE=2：3，求cos∠ABC的值；

（3）如果∠ABC是锐角，且△ABC与△ADE相似，求∠ABC的度数.

Answer 1

【答案】（1）证明见详解；（2）；（3）30°或45°.

【解析】

（1）由题意：∠E=90°-∠ADE，证明∠ADE=90°- ∠C即可解决问题．

(2) 延长AD交BC于点F．证明AE∥BC，可得∠AFB=∠EAD=90°，，由BD：DE=2：3，可得cos∠ABC= ；

（3）因为△ABC与△ADE相似，∠DAE=90°，所以∠ABC中必有一个内角为90°因为∠ABC是锐角，推出∠ABC≠90°．接下来分两种情形分别求解即可．

（1）证明：如图1中，

∵AE⊥AD，

∴∠DAE=90°，∠E=90°-∠ADE，

∵AD平分∠BAC，

∴∠BAD= ∠BAC，同理∠ABD= ∠ABC，

∵∠ADE=∠BAD+∠DBA，∠BAC+∠ABC=180°-∠C，

∴∠ADE= （∠ABC+∠BAC）=90°- ∠C，

∴∠E=90°-（90°- ∠C）= ∠C．

（2）解：延长AD交BC于点F．

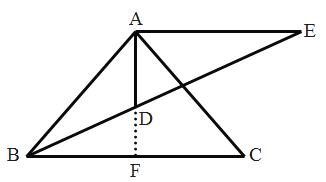
∵AB=AE，

∴∠ABE=∠E，

BE平分∠ABC，

∴∠ABE=∠EBC，

∴∠E=∠CBE，

∴AE∥BC，

∴∠AFB=∠EAD=90°，，

∵BD：DE=2：3，

∴cos∠ABC=；

(3）∵△ABC与△ADE相似，∠DAE=90°，

∴∠ABC中必有一个内角为90°

∵∠ABC是锐角，

∴∠ABC≠90°．

①当∠BAC=∠DAE=90°时，

∵∠E=∠C，

∴∠ABC=∠E=∠C，

∵∠ABC+∠C=90°，

∴∠ABC=30°；

②当∠C=∠DAE=90°时，∠E＝∠C=45°，

∴∠EDA=45°，

∵△ABC与△ADE相似，

∴∠ABC=45°；

综上所述，∠ABC=30°或45°.