题目内容
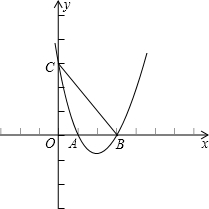
如图,抛物线y=ax2+bx+3经过点A(1,0)和B(3,0),点C(m,
)在抛物线的对称轴上.
(1)求抛物线的函数表达式.
(2)求证:△ABC是等腰三角形.
(3)动点P在线段AC上,从点A出发以每钞1个单位的速度向C运动,同时动点Q在线段AB上,从B出发以每秒1个单位的速度向A运动.当Q到达点A时,两点同时停止运动.设运动时间为t秒,求当t为何值时,△APQ与△ABC相似.

| 15 |
(1)求抛物线的函数表达式.
(2)求证:△ABC是等腰三角形.
(3)动点P在线段AC上,从点A出发以每钞1个单位的速度向C运动,同时动点Q在线段AB上,从B出发以每秒1个单位的速度向A运动.当Q到达点A时,两点同时停止运动.设运动时间为t秒,求当t为何值时,△APQ与△ABC相似.

(1)把A(1,0)和B(3,0)代入y=ax2+bx+3得:
,
解得:
,
∴抛物线的函数解析式是y=x2-4x+3.
(2)抛物线的对称轴是x=2,
∵点C(m,
)在抛物线对称轴上,
∴m=2,
∴点C(2,
),
∴CA=
=4,CB=
=4,
∴CA=CB
∴△ABC是等腰三角形.
(3)∠A是公共角,
①当∠APQ=∠ACB时,△APQ∽△ACB,
∵AB=2,AC=4,AP=t,AQ=2-t,
∴
=
,
解得:t=
.
②当∠APQ=∠ABC时,△APQ∽△ABC,
∵AB=2,AC=4,AP=t,AQ=2-t,
∴
=
,
∴t=
,
∴当t=
或t=
时,△APQ与△ABC相似.
|
解得:
|
∴抛物线的函数解析式是y=x2-4x+3.
(2)抛物线的对称轴是x=2,
∵点C(m,
| 15 |
∴m=2,
∴点C(2,
| 15 |
∴CA=
| 1+15 |
| 1+15 |
∴CA=CB
∴△ABC是等腰三角形.
(3)∠A是公共角,
①当∠APQ=∠ACB时,△APQ∽△ACB,
∵AB=2,AC=4,AP=t,AQ=2-t,
∴
| t |
| 4 |
| 2-t |
| 2 |
解得:t=
| 4 |
| 3 |
②当∠APQ=∠ABC时,△APQ∽△ABC,
∵AB=2,AC=4,AP=t,AQ=2-t,
∴
| t |
| 2 |
| 2-t |
| 4 |
∴t=
| 2 |
| 3 |
∴当t=
| 4 |
| 3 |
| 2 |
| 3 |

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
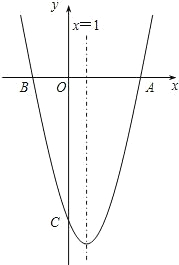 段OC的长度是线段OA的2倍,抛物线的对称轴是直线x=1.
段OC的长度是线段OA的2倍,抛物线的对称轴是直线x=1.


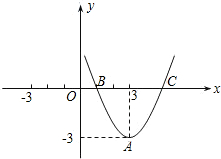 面积等于以点A、P0、B、C为顶点的四边形面积的三分之一?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
面积等于以点A、P0、B、C为顶点的四边形面积的三分之一?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.