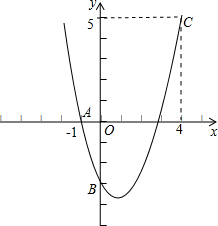题目内容
如图,在平面直角坐标系中,二次函数y=-
x2+bx经过点O、A、B三点,且A点坐标为(4,0),B的坐标为(m,2
),点C是抛物线在第三象限的一点,且横坐标为-2
(1)求抛物线的解析式和直线BC的解析式.
(2)直线BC与x轴相交于点D,求△OBC的面积.

| ||
| 2 |
| 3 |
(1)求抛物线的解析式和直线BC的解析式.
(2)直线BC与x轴相交于点D,求△OBC的面积.

(1)将点A的坐标代入抛物线的解析式中,得:
-
×16+4b=0,b=2
∴抛物线的解析式:y=-
x2+2
x;
∴B(2,2
)、C(-2,-6
)
设直线BC的解析式为:y=kx+b,代入B、C点的坐标,得:
,
解得
故直线BC的解析式:y=2
x-2
.
(2)由直线BC:y=2
x-2
知:D(1,0);
则S△OBC=
OD×|yB-yC|=
×1×8
=4
.
-
| ||
| 2 |
| 3 |
∴抛物线的解析式:y=-
| ||
| 2 |
| 3 |
∴B(2,2
| 3 |
| 3 |
设直线BC的解析式为:y=kx+b,代入B、C点的坐标,得:
|
解得
|
故直线BC的解析式:y=2
| 3 |
| 3 |
(2)由直线BC:y=2
| 3 |
| 3 |
则S△OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目