题目内容
【题目】如图，在四边形ABCD中，AD∥BC，若∠DAB的平分线AE交CD于E，连结BE，且BE也平分∠ABC，则以下的命题中正确的个数是（ ）
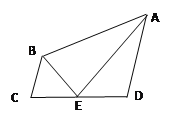
①BC+AD=AB ； ②Ｅ为CD中点
③∠AEB=90°； ④S△ABE=
S四边形ABCD
A.1B.2C.3D.4
【答案】D
【解析】
在AB上截取AF=AD．证明△AED≌△AEF，△BEC≌△BEF．可证4个结论都正确．
解：在AB上截取AF=AD．
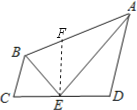
则△AED≌△AEF（SAS）．
∴∠AFE=∠D．
∵AD∥BC，∴∠D+∠C=180°．
∴∠C=∠BFE．
∴△BEC≌△BEF（AAS）．
∴①BC=BF，故AB=BC+AD；
②CE=EF=ED，即E是CD中点；
③∠AEB=∠AEF+∠BEF=
∠DEF+∠CEF=×180°=90°；
④S△AEF=S△AED，S△BEF=S△BEC，
∴S△AEB=S四边形BCEF+S四边形EFAD=S四边形ABCD．
故选D．
练习册系列答案
相关题目
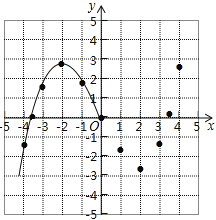
【题目】某学习小组在研究函数y=
x3﹣2x的图象与性质时，已列表、描点并画出了图象的一部分．
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
（1）请补全函数图象；
（2）方程
x3﹣2x=﹣2实数根的个数为 ；
（3）观察图象，写出该函数的两条性质．
