题目内容
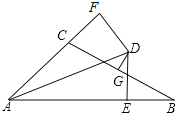
【题目】已知∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,
(1)连接CD、BD,求证:△CDF≌△BDE;
(2)若AE=5,AC=3,求BE的长.
【答案】(1)证明见解析;(2)2.
【解析】
(1)连CD、BD,如图,根据角平行线的性质定理得到DE=DF,根据线段垂直平分线的性质得CD=BD,则可利用“HL“证明Rt△CDF≌Rt△BDE;
(2)先证明Rt△ADF≌Rt△ADE得到AE=AF,再由Rt△CDF≌Rt△BDE得出BE=CF,进而解答即可.
证明:(1)如图,连接CD、BD,
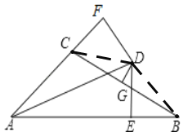
∵AD平分∠BAE,DE⊥AB,DF⊥AC,
∴DE=DF,
又∵DG垂直平分BC,
∴CD=BD,
在Rt△CDF和Rt△BDE中
∵![]() ,
,
∴Rt△CDF≌Rt△BDE(HL),
(2)在Rt△ADF和Rt△ADE中
∵![]() ,
,
∴Rt△ADF≌Rt△ADE(HL),
∴AE=AF,
∵Rt△CDF≌Rt△BDE,
∴BE=CF,
∵CF=AF﹣AC=5﹣3=2,
∴BE=2.

 阅读快车系列答案
阅读快车系列答案【题目】主题班会上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟.根据同学们的选择情况,小明绘制了下面两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
观点 | 频数 | 频率 |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |
(1)参加本次讨论的学生共有 人;表中a= ,b= ;
(2)在扇形统计图中,求D所在扇形的圆心角的度数;
(3)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.




