题目内容
【题目】已知二次函数![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴的交点为
轴的交点为![]() ,顶点部分为
,顶点部分为![]() ,若点
,若点![]() 是四边形
是四边形![]() 边上的点,则
边上的点,则![]() 的最大值为( )
的最大值为( )
A. -6 B. -8 C. -12 D. -18
【答案】A
【解析】
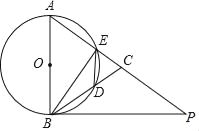
令y=0,求得与x轴的交点坐标,令x=0,求得与y轴的交点坐标,根据顶点式解析式得顶点坐标,设z=3x-y,则y=3x-z.如图由函数y=3x-z的图象可知,欲求z的最大值,可以转化为求直线y=3x-z与y轴交点的纵坐标的最小值即可.
令y=0,则x2+8x+12=0,
解得:x1=-2,x2=-6,
∵点A在点C的左侧,
∴A(-6,0)、C(-2,0),
令x=0,则y=12,
与y轴交点坐标为B(0,12),
∵y=(x+4)2-4
∴顶点坐标D为(-4,-4).
设z=3x-y,则y=3x-z.
如图由函数y=3x-z的图象可知,欲求z的最大值,可以转化为求直线y=3x-z与y轴交点的纵坐标的最小值即可,
由图象可知当直线经过点C时-z的值最小,z的值最大,
把(-2,0)代入y=3x-z,得到z=-6,
∴z的最大值为-6.
故选:A

练习册系列答案
相关题目