题目内容
【题目】如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)求该抛物线所对应的函数解析式;
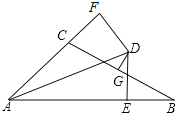
(2)如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.

【答案】(1)y=﹣x2+2x+3;(2)①S四边形ACFD= 4;②Q点坐标为(1,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由A、B两点的坐标,利用待定系数法即可求得抛物线解析式;
(2)①连接CD,则可知CD∥x轴,由A、F的坐标可知F、A到CD的距离,利用三角形面积公式可求得△ACD和△FCD的面积,则可求得四边形ACFD的面积;②由题意可知点A处不可能是直角,则有∠ADQ=90°或∠AQD=90°,当∠ADQ=90°时,可先求得直线AD解析式,则可求出直线DQ解析式,联立直线DQ和抛物线解析式则可求得Q点坐标;当∠AQD=90°时,设Q(t,-t2+2t+3),设直线AQ的解析式为y=k1x+b1,则可用t表示出k′,设直线DQ解析式为y=k2x+b2,同理可表示出k2,由AQ⊥DQ则可得到关于t的方程,可求得t的值,即可求得Q点坐标.
(1)由题意可得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3;
(2)①∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴F(1,4),
∵C(0,3),D(2,3),
∴CD=2,且CD∥x轴,
∵A(﹣1,0),
∴S四边形ACFD=S△ACD+S△FCD=![]() ×2×3+
×2×3+![]() ×2×(4﹣3)=4;
×2×(4﹣3)=4;
②∵点P在线段AB上,
∴∠DAQ不可能为直角,
∴当△AQD为直角三角形时,有∠ADQ=90°或∠AQD=90°,
i.当∠ADQ=90°时,则DQ⊥AD,
∵A(﹣1,0),D(2,3),
∴直线AD解析式为y=x+1,
∴可设直线DQ解析式为y=﹣x+b′,
把D(2,3)代入可求得b′=5,
∴直线DQ解析式为y=﹣x+5,
联立直线DQ和抛物线解析式可得![]() ,解得
,解得![]() 或
或![]() ,
,
∴Q(1,4);
ii.当∠AQD=90°时,设Q(t,﹣t2+2t+3),
设直线AQ的解析式为y=k1x+b1,
把A、Q坐标代入可得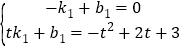 ,解得k1=﹣(t﹣3),
,解得k1=﹣(t﹣3),
设直线DQ解析式为y=k2x+b2,同理可求得k2=﹣t,
∵AQ⊥DQ,
∴k1k2=﹣1,即t(t﹣3)=﹣1,解得t=![]() ,
,
当t=![]() 时,﹣t2+2t+3=
时,﹣t2+2t+3=![]() ,
,
当t=![]() 时,﹣t2+2t+3=
时,﹣t2+2t+3=![]() ,
,
∴Q点坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
综上可知Q点坐标为(1,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案