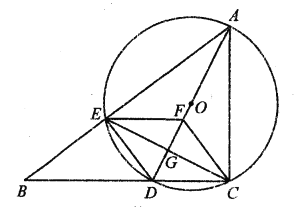
题目内容
【题目】已知正方形![]() 中,
中,![]() 为对角线
为对角线![]() 上一点,过点
上一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(1)如图1,求证:![]() ;
;
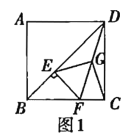
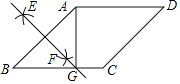
(2)将图1中的![]() 绕点
绕点![]() 逆时针旋转45°,如图2,取
逆时针旋转45°,如图2,取![]() 的中点
的中点![]() ,连接
,连接![]() .问(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
.问(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
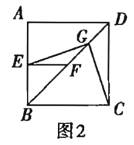
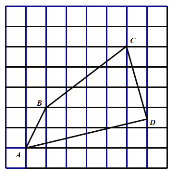
(3)将图1中的![]() 绕点
绕点![]() 逆时计旋转任意角度,如图3,取
逆时计旋转任意角度,如图3,取![]() 的中点
的中点![]() ,连接
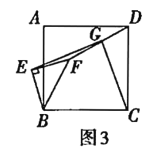
,连接![]() .问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
.问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.
(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.
(3)结论依然成立.过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N.由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC,得出△MEC是等腰直角三角形,就可以得出结论.
(1)在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
同理,在![]() 中,
中,![]() .
.
∴![]() .
.
(2)如图②,(1)中结论仍然成立,即EG=CG.
理由:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.
∴∠AMG=∠DMG=90°.
∵四边形ABCD是正方形,
∴AD=CD=BC=AB,∠ADG=∠CDG.∠DAB=∠ABC=∠BCD=∠ADC=90°.
在△DAG和△DCG中,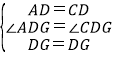 ,
,
∴△DAG≌△DCG(SAS),
∴AG=CG.
∵G为DF的中点,
∴GD=GF.
∵EF⊥BE,
∴∠BEF=90°,
∴∠BEF=∠BAD,
∴AD∥EF,
∴∠N=∠DMG=90°.
在△DMG和△FNG中,
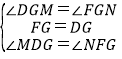 ,
,
∴△DMG≌△FNG(ASA),
∴MG=NG.
∵∠DA∠AMG=∠N=90°,
∴四边形AENM是矩形,
∴AM=EN,
在△AMG和△ENG中,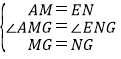 ,
,
∴△AMG≌△ENG(SAS),
∴AG=EG,
∴EG=CG;
(3)如图③,(1)中的结论仍然成立.
理由:过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN⊥AB于N.
∵MF∥CD,
∴∠FMG=∠DCG,∠MFD=∠CDG.∠AQF=∠ADC=90°
∵FN⊥AB,
∴∠FNH=∠ANF=90°.
∵G为FD中点,
∴GD=GF.
在△MFG和△CDG中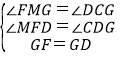 ,
,
∴△CDG≌△MFG(AAS),
∴CD=FM.MG=CG.
∴MF=AB.
∵EF⊥BE,
∴∠BEF=90°.
∵∠NHF+∠HNF+∠NFH=∠BEF+∠EHB+∠EBH=180°,
∴∠NFH=∠EBH.
∵∠A=∠ANF=∠AMF=90°,
∴四边形ANFQ是矩形,
∴∠MFN=90°.
∴∠MFN=∠CBN,
∴∠MFN+∠NFE=∠CBN+∠EBH,
∴∠MFE=∠CBE.
在△EFM和△EBC中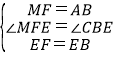 ,
,
∴△EFM≌△EBC(SAS),
∴ME=CE.,∠FEM=∠BEC,
∵∠FEC+∠BEC=90°,
∴∠FEC+∠FEM=90°,
即∠MEC=90°,
∴△MEC是等腰直角三角形,
∵G为CM中点,
∴EG=CG,EG⊥CG.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案