题目内容
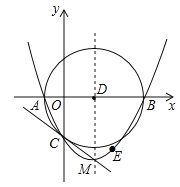
【题目】如图,抛物线y=![]() (x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
(x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】①根据抛物线的解析式得出抛物线与x轴的交点A、B坐标,由抛物线的对称性即可判定;②求得⊙D的直径AB的长,得出其半径,由圆的面积公式即可判定;③过点C作CE∥AB,交抛物线于E,如果CE=AD,则根据一组等边平行且相等的四边形是平行四边形即可判定;④求得直线CM、直线CD的解析式通过它们的斜率进行判定.
∵在y=![]() (x+2)(x﹣8)中,当y=0时,x=﹣2或x=8,
(x+2)(x﹣8)中,当y=0时,x=﹣2或x=8,
∴点A(﹣2,0)、B(8,0),
∴抛物线的对称轴为x=![]() =3,故①正确;
=3,故①正确;
∵⊙D的直径为8﹣(﹣2)=10,即半径为5,
∴⊙D的面积为25π,故②错误;
在y=![]() (x+2)(x﹣8)=
(x+2)(x﹣8)=![]() x2﹣
x2﹣![]() x﹣4中,当x=0时y=﹣4,
x﹣4中,当x=0时y=﹣4,
∴点C(0,﹣4),
当y=﹣4时,![]() x2﹣
x2﹣![]() x﹣4=﹣4,
x﹣4=﹣4,
解得:x1=0、x2=6,
所以点E(6,﹣4),
则CE=6,
∵AD=3﹣(﹣2)=5,
∴AD≠CE,
∴四边形ACED不是平行四边形,故③错误;
∵y=![]() x2﹣
x2﹣![]() x﹣4=
x﹣4=![]() (x﹣3)2﹣
(x﹣3)2﹣![]() ,
,
∴点M(3,﹣![]() ),
),
∴DM=![]() ,
,
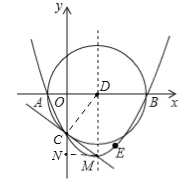
如图,连接CD,过点M作MN⊥y轴于点N,则有N(0,﹣![]() ),MN=3,
),MN=3,
∵C(0,-4),∴CN=![]() ,∴CM2=CN2+MN2=
,∴CM2=CN2+MN2=![]() ,
,
在Rt△ODC中,∠COD=90°,∴CD2=OC2+OD2=25,∴CM2+CD2=![]() ,
,
∵DM2=![]() ,
,
∴CM2+CD2=DM2,
∴∠DCM=90°,即DC⊥CM,
∵CD是半径,
∴直线CM与⊙D相切,故④正确,
故选B.

 新思维寒假作业系列答案
新思维寒假作业系列答案【题目】如图,这是网上盛传的一个关于数学的诡辩问题截图,表1是它的示意表.我们一起来解答“为什么多出了![]() 元”.
元”.

表1
花去 | 剩余 | |
买牛肉 |
|
|
买猪脚 |
|
|
买蔬菜 |
|
|
买调料 |
|
|
总计 |
|
|
(1)为了解释“剩余金额总计”与“我手里有![]() 元”无关,按要求填写表2中的空格.
元”无关,按要求填写表2中的空格.
表2
花去 | 剩余 | |
买牛肉 |
|
|
买猪脚 |
|
|
买蔬菜 | 元 | 元 |
买调料 | 元 |
|
总计 |
|
|
表3
花去 | 剩余 | |
买物品1 |
|
|
买物品2 |
|
|
买物品3 |
|
|
买物品4 |
|
|
总计 |
|
|
(2)如表3中,直接写出以下各代数式的值:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(3)如表3中,![]() 都是正整数,则
都是正整数,则![]() 的最大值等于 ;最小值等于 .由此可以知道“为什么多出了
的最大值等于 ;最小值等于 .由此可以知道“为什么多出了![]() 元”只是一个诡辩而已.
元”只是一个诡辩而已.
(4)我们将“花去”记为“![]() ”,“剩余”记为“
”,“剩余”记为“![]() ”,请在表4中将表1数据重新成号.
”,请在表4中将表1数据重新成号.
花去 | 剩余 | |
买牛肉 | 元 | 元 |
买猪脚 | 元 | 元 |
买蔬菜 | 元 | 元 |
买调料 | 元 | 元 |
总计 | 元 |