��Ŀ����
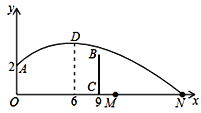
����Ŀ������[a��b��c]Ϊ����y=ax2+bx+c�����������������������Ϊ[m��1��1+m����2m]�ĺ�����һЩ���ۣ��ٵ�m=3ʱ������ͼ��Ķ��������ǣ���1����8�����ڵ�m��1ʱ������ͼ���x�����õ��߶γ��ȴ���3���۵�m��0ʱ��������x��![]() ʱ��y��x���������С���ܲ���mȡ��ֵ������ͼ���������㣮������ȷ�Ľ����У�������
ʱ��y��x���������С���ܲ���mȡ��ֵ������ͼ���������㣮������ȷ�Ľ����У�������
A. 1�� B. 2�� C. 3�� D. 4��
���𰸡�D
��������
�����������ߵĶ�������Ϊ��![]() ��
��![]() ������m=3ʱ��������Ϊ[2,4-6]������ö�������Ϊ��-1��-8������������ȷ��������ͼ����x�ύ������Ϊ��
������m=3ʱ��������Ϊ[2,4-6]������ö�������Ϊ��-1��-8������������ȷ��������ͼ����x�ύ������Ϊ��![]() ����������Ϊ [m-1��1+ m ��-2m]�ĺ�����x�ύ������ֱ�Ϊ��1,0������
����������Ϊ [m-1��1+ m ��-2m]�ĺ�����x�ύ������ֱ�Ϊ��1,0������![]() ��0�������Խص�x�����õ��߶γ�Ϊ1-
��0�������Խص�x�����õ��߶γ�Ϊ1-![]() =1+
=1+![]() �� ��m > 1 ʱ�� 1+
�� ��m > 1 ʱ�� 1+![]() >3����������ȷ���������Գ���Ϊx=
>3����������ȷ���������Գ���Ϊx=![]() =
=![]() �� ��m<0ʱ���Գ���x=
�� ��m<0ʱ���Գ���x=![]() <
<![]() ��a=m-1<0,���Ժ���������ͼ�����£���x>
��a=m-1<0,���Ժ���������ͼ�����£���x>![]() ʱy��x���������С������Ϊx=
ʱy��x���������С������Ϊx=![]() <
<![]() �����Ե�m < 0ʱ��������x >
�����Ե�m < 0ʱ��������x >![]() ʱ��y��x���������С������ȷ���� ����mȡ��ֵ������ͼ���������㣨1,0���ͣ�-2��-6������������ȷ����ѡD
ʱ��y��x���������С������ȷ���� ����mȡ��ֵ������ͼ���������㣨1,0���ͣ�-2��-6������������ȷ����ѡD

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�