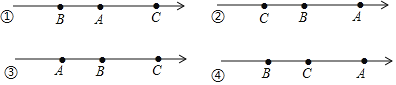
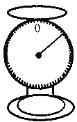
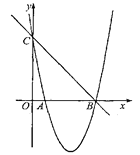
��Ŀ����
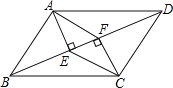
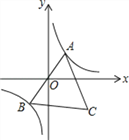
����Ŀ����֪,����ABCD��,AB=4cm,BC=8cm,AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E. F,����ΪO.

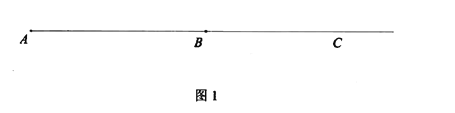
(1)��ͼ1������AF��CE.��֤���ı���AFCEΪ����.
(2)��ͼ1����AF�ij�.
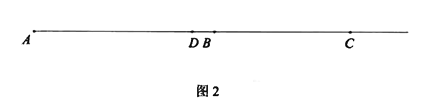
(3)��ͼ2������P��Q�ֱ��A. C����ͬʱ�������ء�AFB�͡�CDE���������˶�һ�ܡ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У���P���ٶ�Ϊÿ��1cm�����˶�ʱ��Ϊt��.
�������˶��Ĺ����У���A. P��C. Q�ĵ�Ϊ������ı����п����Ǿ�����?���п��ܣ�������˶�ʱ��t�͵�Q���ٶȣ��������ܣ���˵������.
������Q���ٶ�Ϊÿ��0.8cm����A. P��C. Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ.
���𰸡���1������������2��AF=5cm����3����P���˶���ʱ���� 8��Q���ٶ���0.5cm/s����t=![]() .
.
��������
��1��֤��AEO�ա�CFO���Ƴ�OE=OF������ƽ���ı��κ����ε��ж��Ƴ����ɣ�
��2����AF=CF=a�����ݹ��ɶ����ó�����a�ķ��̣�������ɣ�
��3����ֻ�е�P�˶���B�㣬Q�˶���D��ʱ����A��P��C��Q�ĵ�Ϊ������ı����п����Ǿ��Σ����ʱ��t����������𰸣��ڷ�Ϊ���������P��AF�ϣ�P��BF�ϣ�P��AB�ϣ�����ƽ���ı��ε�����������ɣ�
(1)֤�������ı���ABCD�Ǿ��Σ�
��AD��BC��
���AEO=��CFO��
��AC�Ĵ�ֱƽ����EF��
��AO=OC��AC��EF��
����AEO����CFO��
�� ��
��
���AEO�ա�CFO(AAS)��
��OE=OF��
��OA=OC��
���ı���AECF��ƽ���ı��Σ�
��AC��EF��
��ƽ���ı���AECF�����Σ�
(2)��AF=acm��
���ı���AECF�����Σ�
��AF=CF=acm��
��BC=8cm��
��BF=(8a)cm��
��Rt��ABF��,�ɹ��ɶ����ã�4![]() +(8a)
+(8a) ![]() =a
=a![]() ��
��
a=5��
��AF=5cm��
(3)�����˶������У���A. P��C. Q�ĵ�Ϊ������ı����п����Ǿ��Σ�
ֻ�е�P�˶���B�㣬Q�˶���D��ʱ����A. P��C. Q�ĵ�Ϊ������ı����п����Ǿ��Σ�
P���˶���ʱ���ǣ�(5+3)��1=8��
Q���ٶ��ǣ�4��8=0.5��
��Q���ٶ���0.5cm/s��
�ڷ�Ϊ���������
��һ��P��AF�ϣ�
��P���ٶ���1cm/s����Q���ٶ���0.8cm/s��
��Qֻ����CD�ϣ���ʱ��A. P��C. Q�ĵ�Ϊ������ı��β���ƽ���ı��Σ�
�ڶ�����P��BF��ʱ,Q��CD��DE��,ֻ�е�Q��DE��ʱ,��A. P��C. Q�ĵ�Ϊ������ı��β��п�����ƽ���ı���,��ͼ,

��AQ=8(0.8t4),CP=5+(t5)��
��8(0.8t4)=5+(t5)��
t=![]() ��
��
�����������P��AB��ʱ��Q��DE��CE�ϣ���ʱ��A. P��C. Q�ĵ�Ϊ������ı��β���ƽ���ı��Σ�
��t=![]() .
.
������������A. P��C. Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ,t=![]() .
.