Question

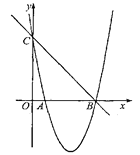
【题目】如图，已知抛物线y＝x2＋bx＋c的图像与x轴的一个交点为A(1，0)，另一个交点为B，且与y轴交于点C(0，5)．

(1)求直线BC及抛物线的解析式；

(2)若点M是抛物线在x轴下方图像上的一动点，过点M作MN∥y轴交直线BC于点N，求MN的最大值；

(3)在(2)的条件下，MN取得最大值时，若点P是抛物线在x轴下方图像上任意一点，以BC为边作□CBPQ，设□CBPQ的面积为S1，△ABN的面积为S2，且S1＝6S2，求点P的坐标．

Answer 1

【答案】(1)y＝－x＋5, y＝x2－6x＋5;(2); (3)点P的坐标为P1(2，－3)（与点D重合）或P2(3，－4)．

【解析】分析：（1）根据待定系数法，可得函数解析式，

（2）根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得二次函数，根据二次函数的性质，可由顶点式求解；

（3）先求出△ABN的面积和BC的长，再根据平行四边形的面积和△ABN的面积的关系，可得平行四边形高的长，根据等腰直角三角形，可得CE的长，根据待定系数法，可得PQ的解析式，根据解方程可得答案．

详解：(1)∵抛物线y＝x2＋bx＋c与x轴的一个交点为A(1，0)，与y轴交于点C(0，5)，

∴将A(1，0)，C(0，5)代入y＝x2＋bx＋c，

解得：b＝－6，c＝5.

∴二次函数解析式为：y＝x2－6x＋5.

令y=0，求得另一交点B的坐标为（5，0）

设直线BC的解析式为：y＝kx＋5.

将B(5，0)代入直线BC解析式y＝kx＋5.

解得：k＝－1.

∴直线BC的解析式为：y＝－x＋5.

(2)如图①.设M(x，y)，则

NM＝－x＋5－(x2－6x＋5).

NM＝－x2＋5x.

NM＝－(x－)2＋.

∴NM的最大值为.

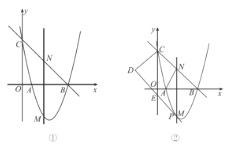
（3）如图②由第2问易得S2＝5，∴S1＝6S2＝30.

BC＝5，BC所在直线的解析式为：y＝－x＋5，

∠CBO＝45°，

∵S2＝30.∴平行四边形CBPQ中BC边上的高为.

过点C作CD⊥PQ与PQ所在直线相交于点D，

PD交y轴于点E，CD＝3，∴CE＝6，

∵平行四边形CBPQ的边PQ所在直线，在直线BC的两侧可能各有一条，但点P在x轴下方，

∴PQ的解析式为y＝－x－1.

∵点P同时在抛物线和直线PQ上，

∴x2－6x＋5＝－x－1.解得x1＝2，x2＝3，

∴P1(2，－3)，P2(3，－4).