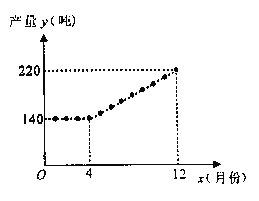
题目内容
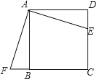
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿斜面坡度
米处的点C出发,沿斜面坡度![]() 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .计算结果保留根号)
.计算结果保留根号)
【答案】3![]() +3.5
+3.5
【解析】
试题分析:延长ED交BC延长线于点F,则∠CFD=90°,Rt△CDF中求得CF=CDcos∠DCF=2![]() 、DF=
、DF=![]() CD=2,作EG⊥AB,可得GE=BF=4
CD=2,作EG⊥AB,可得GE=BF=4![]() 、GB=EF=3.5,再求出AG=GEtan∠AEG=4
、GB=EF=3.5,再求出AG=GEtan∠AEG=4![]() tan37°可得答案.
tan37°可得答案.
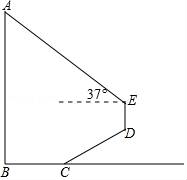
试题解析:如图,延长ED交BC延长线于点F,则∠CFD=90°,

∵tan∠DCF=i=![]() =
=![]() ,
,
∴∠DCF=30°,
∵CD=4,
∴DF=![]() CD=2,CF=CDcos∠DCF=4×
CD=2,CF=CDcos∠DCF=4×![]() =2
=2![]() ,
,
∴BF=BC+CF=2![]() +2
+2![]() =4
=4![]() ,
,
过点E作EG⊥AB于点G,
则GE=BF=4![]() ,GB=EF=ED+DF=1.5+2=3.5,
,GB=EF=ED+DF=1.5+2=3.5,
又∵∠AED=37°,
∴AG=GEtan∠AEG=4![]() tan37°,
tan37°,
则AB=AG+BG=4![]() tan37°+3.5=3
tan37°+3.5=3![]() +3.5,
+3.5,
故旗杆AB的高度为(3![]() +3.5)米.
+3.5)米.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目