题目内容
【题目】在平面直角坐标系中,点A(0,2)、B(a,a+2)、C(b,0)(a>0,b>0),若AB=![]() 且∠ACB最大时,b的值为( )
且∠ACB最大时,b的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
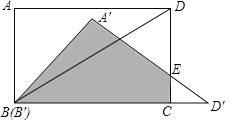
根据圆周角大于对应的圆外角可得当![]() 的外接圆与
的外接圆与![]() 轴相切时,
轴相切时,![]() 有最大值,此时圆心F的横坐标与C点的横坐标相同,并且在经过AB中点且与直线AB垂直的直线上,根据FB=FC列出关于b的方程求解即可.
有最大值,此时圆心F的横坐标与C点的横坐标相同,并且在经过AB中点且与直线AB垂直的直线上,根据FB=FC列出关于b的方程求解即可.
解:∵AB=![]() ,A(0,2)、B(a,a+2)
,A(0,2)、B(a,a+2)
∴![]() ,
,
解得a=4或a=-4(因为a>0,舍去)
∴B(4,6),
设直线AB的解析式为y=kx+2,
将B(4,6)代入可得k=1,所以y=x+2,
利用圆周角大于对应的圆外角得当![]() 的外接圆与
的外接圆与![]() 轴相切时,
轴相切时,![]() 有最大值.
有最大值.
如下图,G为AB中点,![]() ,
,
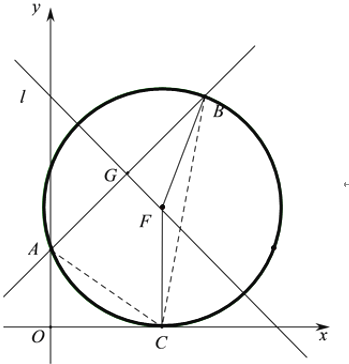
设过点G且垂直于AB的直线![]() ,
,
将![]() 代入可得
代入可得![]() ,所以
,所以![]() .
.
设圆心![]() ,由
,由![]() ,可知
,可知![]() ,解得
,解得![]() (已舍去负值).
(已舍去负值).
故选:B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
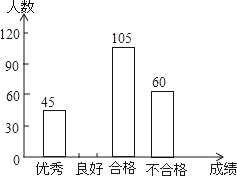
【题目】为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
成绩 | 频数 | 频率 |
优秀 | 45 | b |
良好 | a | 0.3 |
合格 | 105 | 0.35 |
不合格 | 60 | c |
(1)该校初三学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.