题目内容
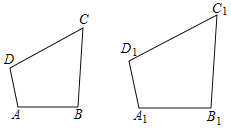
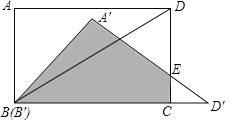
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,连接BD,将△ABD绕B点作顺时针方向旋转得到△A′B′D′(B′与B重合),且点D′刚好落在BC的延长上,A′D′与CD相交于点E.
(1)求矩形ABCD与△A′B′D′重叠部分(如图中阴影部分A′B′CE)的面积;
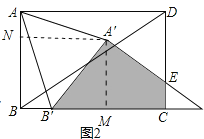
(2)将△A′B′D′以2cm/s的速度沿直线BC向右平移,当B′移动到C点时停止移动.设矩形ABCD与△A′B′D′重叠部分的面积为ycm2,移动的时间为x秒,请你求出y关于x的函数关系式,并指出自变量x的取值范围.
【答案】(1)![]() ;(2)当0≤x<
;(2)当0≤x<![]() 时,y=﹣
时,y=﹣![]() x2﹣
x2﹣![]() x+24,当
x+24,当![]() ≤x≤4时,y=
≤x≤4时,y=![]() x2-
x2-![]() x+
x+![]()
【解析】
(1)根据旋转的性质可知B′D′=BD=10,CD′=B′D′﹣BC=2,由tan∠B′D′A′=![]() ,可求出CE,即可计算△CED′的面积,SA′B′CE=SA′B′D′﹣SCED′;
,可求出CE,即可计算△CED′的面积,SA′B′CE=SA′B′D′﹣SCED′;
(2)分类讨论,当0≤x≤![]() 时和当
时和当 ![]() <x≤4时,分别列出函数表达式;
<x≤4时,分别列出函数表达式;
解:(1)∵AB=6cm,AD=8cm,
∴BD=10cm,
根据旋转的性质可知B′D′=BD=10cm,CD′=B′D′﹣BC=2cm,
∵tan∠B′D′A=![]() ,
,
∴![]() ,
,
∴CE=![]() cm,
cm,
∴S A′B′CE=SA′B′D′﹣SCED′=![]() ﹣2×
﹣2×![]() ÷2=
÷2=![]() (cm2);
(cm2);
(2)①当0≤x<![]() 时,CD′=2x+2,CE=
时,CD′=2x+2,CE=![]() x,
x,
∴S△CD′E=![]() x2+
x2+![]() x,
x,
∴y=![]() ×6×8﹣
×6×8﹣![]() x2﹣
x2﹣![]() x=﹣
x=﹣![]() x2﹣
x2﹣![]() x+24;
x+24;
②当![]() ≤x≤4时,B′C=10﹣2x,CE=
≤x≤4时,B′C=10﹣2x,CE=![]() (10﹣2x)
(10﹣2x)
∴y=![]() ×
×![]() (10﹣2x)2=
(10﹣2x)2=![]() x2-
x2-![]() x+
x+![]() .
.

练习册系列答案
相关题目