Question

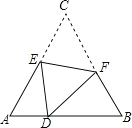
【题目】如图，D是等边△ABC边AB上的一点，且AD：DB=1：2，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上，则CE：CF=（ ）

A． B． C． D．

Answer 1

【答案】B

【解析】

试题分析：借助翻折变换的性质得到DE=CE；设AB=3k，CE=x，则AE=3k﹣x；根据相似三角形的判定与性质即可解决问题．

解：设AD=k，则DB=2k，

∵△ABC为等边三角形，

∴AB=AC=3k，∠A=∠B=∠C=∠EDF=60°，

∴∠EDA+∠FDB=120°，

又∵∠EDA+∠AED=120°，

∴∠FDB=∠AED，

∴△AED∽△BDF，

∴，

设CE=x，则ED=x，AE=3k﹣x，

设CF=y，则DF=y，FB=3k﹣y，

∴，

∴，

∴=，

∴CE：CF=4：5．

故选：B．

解法二：解：设AD=k，则DB=2k，

∵△ABC为等边三角形，

∴AB=AC=3k，∠A=∠B=∠C=∠EDF=60°，

∴∠EDA+∠FDB=120°，

又∵∠EDA+∠AED=120°，

∴∠FDB=∠AED，

∴△AED∽△BDF，由折叠，得

CE=DE，CF=DF

∴△AED的周长为4k，△BDF的周长为5k，

∴△AED与△BDF的相似比为4：5

∴CE：CF=DE：DF=4：5．

故选：B．