题目内容
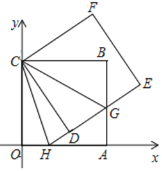
【题目】图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连结AB、AE、BE.已知tan∠CBE= ![]() ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).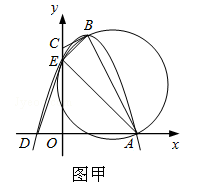
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:设抛物线的解析式为y=a(x+1)(x﹣3).
∵将点E(0,3)代入抛物线的解析式得:﹣3a=3,
∴a=﹣1.
∴抛物线的解析式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3.
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴B(1,4)
(2)
解:如图1所示:过点B作BF⊥y轴,垂足为F.
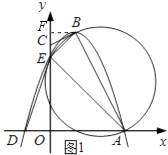
∵A(3,0),E(0,3),
∴OE=OA=3.
∴∠OEA=45°.
∵E(0,3),B(1,4),
∴EF=BF.
∴∠FEB=45°.
∴∠BEA=90°.
∴AB为△ABE的外接圆的直径.
∵∠FEB=∠OEA=45°,∠EOA=∠BFE,
∴△BFE∽△AOE.
∴tan∠EAB= ![]() =
= ![]() .
.
∵tan∠CBE= ![]() ,
,
∴∠CBE=∠EAB.
∵∠EAB+∠EBA=90°,
∴∠CBE+∠EBA=90°,即∠CBA=90°.
∴CB是△ABE的外接圆的切线
(3)
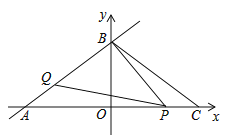
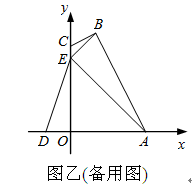
解:如图2所示:
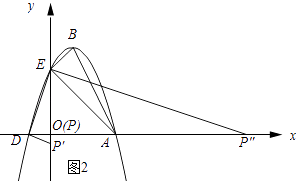
∵ ![]() 且∠DOE=∠BEA=90°,
且∠DOE=∠BEA=90°,
∴△EOD∽△AEB.
∴当点P与点O重合时,△EPD∽△AEB.
∴点P的坐标为(0,0).
过点D作DP′⊥DE,交y轴与点P′.
∵∠P′ED=∠DEO,∠DOE=∠EDP′,
∴△EDP′∽△EOD.
又∵△EOD∽△AEB,
∴△EDP′∽△AEB.
∵∠ODP′+∠OP′D=90°,∠DEP′+∠OP′D=90°,
∴∠ODP′=∠DEP′.
∴ ![]() =
= ![]() ,即
,即 ![]() .
.
∴OP′= ![]() .
.
∴点P′的坐标为(0,﹣ ![]() ).
).
过点E作EP″⊥DE,交x轴与点P″.
∵∠EDP″=∠EDO,∠EOD=∠DEP″,
∴△EDO∽△P″DE.
∵又∵△EOD∽△AEB,
∴△EDP″∽△AEB.
∴∠EP″O=∠BAE.
∴tan∠EP″O= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() .
.
∴OP″=9.
∴P″(9,0).
综上所述,点P的坐标为(0,0)或(0,﹣ ![]() )或(9,0)
)或(9,0)
【解析】(1)设抛物线的解析式为y=a(x+1)(x﹣3),将点E(0,3)代入抛物线的解析式求得a的值,从而可得到抛物线的解析式;(2)过点B作BF⊥y轴,垂足为F.先依据配方法可求得点B的坐标,然后依据点A、B、E三点的坐标可知△BFE和△EAO为等腰直角三角形,从而可证明△BAE为直角三角形,接下来证明△BFE∽△EOA,由相似三角形的性质可证明 ![]() =
= ![]() ,从而可得到∠CBE=∠EAB,于是可证明∠CBA=90°,故此CB是△ABE的外接圆的切线;(3)过点D作DP′⊥DE,交y轴与点P′,过点E作EP″⊥DE,交x轴与点P″.然后证明△DEO、△P′DO、△EP″O均与△BAE相似,然后依据相似三角形的性质分别可求得DO、OP′、OP″的长度,从而可求得点P的坐标.
,从而可得到∠CBE=∠EAB,于是可证明∠CBA=90°,故此CB是△ABE的外接圆的切线;(3)过点D作DP′⊥DE,交y轴与点P′,过点E作EP″⊥DE,交x轴与点P″.然后证明△DEO、△P′DO、△EP″O均与△BAE相似,然后依据相似三角形的性质分别可求得DO、OP′、OP″的长度,从而可求得点P的坐标.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案