题目内容
【题目】如图,直线![]() :
:![]() 交
交![]() 、
、![]() 轴分别为
轴分别为![]() 、
、![]() 两点,
两点,![]() 点与
点与![]() 点关于
点关于![]() 轴对称.动点
轴对称.动点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),满足
重合),满足![]() .
.
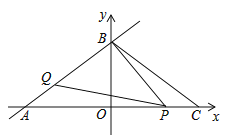
(1)点![]() 坐标是 ,
坐标是 ,![]() .
.
(2)当点![]() 在什么位置时,
在什么位置时,![]() ,说明理由.
,说明理由.
(3)当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,10;(2)当
,10;(2)当![]() 的坐标是
的坐标是![]() 时,
时,![]() ;(3)当
;(3)当![]() 为等腰三角形时,点
为等腰三角形时,点![]() 的坐标是
的坐标是![]() 或
或![]() .
.
【解析】
(1)把x=0和y=0分别代入一次函数的解析式,求出A、B的坐标,根据勾股定理求出BC即可;
(2)求出∠PAQ=∠BCP,∠AQP=∠BPC,根据点的坐标求出AP=BC,根据全等三角形的判定推出即可;
(3)分为三种情况:①PQ=BP,②BQ=QP,③BQ=BP,根据(2)即可推出①,根据三角形外角性质即可判断②,根据勾股定理得出方程,即可求出③.
解:(1)∵![]() ,∴当
,∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,即
,即![]() 的坐标是
的坐标是![]() ,
,![]() 的坐标是
的坐标是![]() ,∵
,∵![]() 点与
点与![]() 点关于
点关于![]() 轴对称,∴
轴对称,∴![]() 的坐标是
的坐标是![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,
由勾股定理得:![]() ,故答案为:
,故答案为:![]() ,10.
,10.
(2)当![]() 的坐标是
的坐标是![]() 时,
时,![]() ,理由是:∵
,理由是:∵![]() ,
,![]() ,∴
,∴![]() ,∵
,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() 和
和![]() 关于
关于![]() 轴对称,∴
轴对称,∴![]() ,
,
在![]() 和
和![]() 中,
中,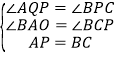 ,∴
,∴![]() ,∴当
,∴当![]() 的坐标是
的坐标是![]() 时,
时,![]() .
.
(3)分为三种情况:
①当![]() 时,∵由(2)知,
时,∵由(2)知,![]() ,∴
,∴![]() ,即此时
,即此时![]() 的坐标是
的坐标是![]() ;
;
②当![]() 时,则
时,则![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
而根据三角形的外角性质得:![]() ,∴此种情况不存在;
,∴此种情况不存在;
③当![]() 时,则
时,则![]() ,即
,即![]() ,设此时
,设此时![]() 的坐标是
的坐标是![]() ,
,
∵在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,
即此时![]() 的坐标是
的坐标是![]() .∴当
.∴当![]() 为等腰三角形时,点
为等腰三角形时,点![]() 的坐标是
的坐标是![]() 或
或![]() .
.
故答案为:(1)![]() ,10;(2)当
,10;(2)当![]() 的坐标是
的坐标是![]() 时,
时,![]() ;(3)当
;(3)当![]() 为等腰三角形时,点
为等腰三角形时,点![]() 的坐标是
的坐标是![]() 或
或![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目