题目内容
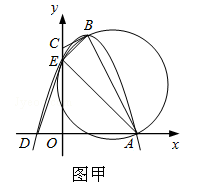
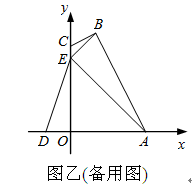
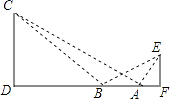
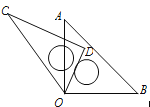
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F. 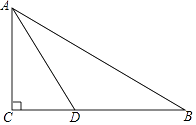
(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD= ![]() ,∠CAD=30°时,求劣弧AD的长.
,∠CAD=30°时,求劣弧AD的长.
【答案】
(1)解:如图所示,
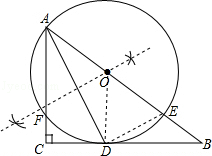
(2)解:证明:连结OD,则OD=OA,
∴∠OAD=∠ODA,
∵∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODC=90°,
即BC⊥OD,
∴BC与⊙O相切
(3)解:如图,连接DE,
∵AE是⊙O的直径,
∴∠ADE=90°,
∵∠OAD=∠ODA=30°,
∴∠AOD=120°,
在Rt△ADE中,AE= ![]() =2,
=2,
∴⊙O的半径=1,
∴劣弧AD的长= ![]() =
= ![]() π
π
【解析】(1)作AD的垂直平分线交AC于O,以AO为半径画圆O分别交AB、AC于点E、F,则⊙O即为所求;(2)连结OD,得到OD=OA,根据等腰三角形的性质得到∠OAD=∠ODA,等量代换得到∠ODA=∠CAD,根据平行线的判定定理得到OD∥AC,根据平行线的性质即可得到结论;(3)连接DE,根据圆周角定理得到∠ADE=90°,根据三角形的内角和得到∠AOD=120°,根据三角函数的定义得到AE=2,根据弧长个公式即可得到结论.
【考点精析】通过灵活运用弧长计算公式,掌握若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的即可以解答此题.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目