��Ŀ����
����Ŀ����ͼ��������y=ax2��6x+c��x�ύ�ڵ�A��B��5��0������y�ύ�ڵ�C��0��5������P���������ϵĶ��㣬���P�ĺ�����Ϊt������PB��PC��PC��x�ύ�ڵ�D������P��y���ƽ���߽�x���ڵ�H����ֱ��BC�ڵ�E��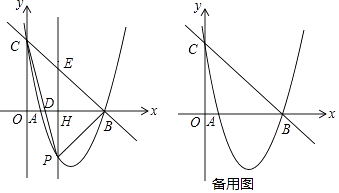
��1���������������Ӧ�ĺ�������ʽ��
��2������P�ڵ������ޣ����BPC�������ֵ��������С�������������ֵ��
��3����t��5ʱ����BPE�ܷ�Ϊ���������Σ����ܣ��������ʱ��P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡�
��1��
�⣺��B��5��0����C��0��5����
��c=5��0=25a��30+c�����a=1��
�������߽���ʽΪy=x2��6x+5��
��2�����
��3��
�⣺���ڣ��������£�
�������֪P��t��t2��6t+5������H��t��0����E��t����t+5�����ҡ�BHEΪ����ֱ�������Σ�
��BE= ![]() BH=
BH= ![]() ��5��t����
��5��t����
�ߡ�BPEΪ���������Σ�
����PE=PB��BE=BP��BE=PE���������
�ٵ�PE=PBʱ�����ڡ�PEB=45�㣬
���PEBΪ����ֱ�������Σ���P��A�㴦����P��1��0�����������⣻
�ڵ�BE=BPʱ������PE��BH��
��HE=HP������E���P����x��Գƣ�
�ੁt+5+t2��6t+5=0�����t=2��t=5���������⣬��ȥ����
��P��2����3����
�۵�BE=PEʱ��
�ߡ�EHBΪ����ֱ�������Σ�
��BE= ![]() HB=
HB= ![]() ��5��t������PE=|��t2+5t|��
��5��t������PE=|��t2+5t|��
��|��t2+5t|= ![]() ��5��t�������t=��
��5��t�������t=�� ![]() ��t=5���������⣬��ȥ����
��t=5���������⣬��ȥ����
��P�� ![]() ��7��6
��7��6 ![]() ����
���� ![]() ��7+6
��7+6 ![]() ����
����
���Ͽ�֪�������������ĵ�P��������Ϊ��1��0����2����3���� ![]() ��7��6
��7��6 ![]() ����
���� ![]() ��7+6
��7+6 ![]() ����
����
����������2����B��5��0����C��0��5����
��ֱ��BC����ʽΪy=��x+5��
��P�ĺ�����Ϊt������PB��PC��PC��x�ύ�ڵ�D������P��y���ƽ���߽�x���ڵ�H����ֱ��BC�ڵ�E��
��P��t��t2��6t+5����E��t����t+5����
��PE=��t+5����t2��6t+5��=��t2+5t��
��S��PBC= ![]() OBPE=
OBPE= ![]() ��5����t2+5t��=��
��5����t2+5t��=�� ![]() ��t��
��t�� ![]() ��2+
��2+ ![]() ��
��
�ߩ� ![]() ��0��
��0��
��S��PBC�����ֵ�����ֵΪ ![]() ��
��
���Դ��ǣ����
�����㾫����������Ŀ����֪���������ö��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�