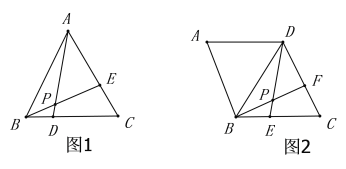Question

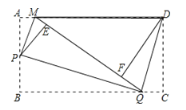
【题目】如图，四边形ABCD中，AB∥CD，∠B=90°，AB=1，CD=2，BC=m，点P是边BC上一动点，若△PAB与△PCD相似，且满足条件的点P恰有2个，则m的值为_______．

Answer 1

【答案】3或2．

【解析】

由平行线得出∠C=90°，当∠BAP=∠CDP时，△PAB∽△PDC，得出 ，得出PC=2PB①，当∠BAP=∠CPD时，△PAB∽△DPC，得出，即PB×PC=1×2=2②，由①②得：PB=1，得出PC=2，BC=3；
设BP=x，则=m-x，得出x：2=1：（m-x），整理得：x2-mx+2=0，方程有唯一解时，△=m2-8=0，解得：m=±2（负值舍去），得出m=2；即可得出结论．

∵AB∥CD，∠B=90°，
∴∠C+∠B=180°，
∴∠C=90°，
当∠BAP=∠CDP时，△PAB∽△PDC，
∴，即，
∴PC=2PB①，
当∠BAP=∠CPD时，△PAB∽△DPC，
∴，即PB×PC=1×2=2②，
由①②得：2PB2=2，
解得：PB=1，
∴PC=2，
∴BC=3；
设BP=x，则=m-x，
∴x：2=1：（m-x），
整理得：x2-mx+2=0，
方程有唯一解时，△=m2-8=0，
解得：m=±2负值舍去），
∴m=2；
综上所述，若△PAB与△PCD相似，且满足条件的点P恰有2个，则m的值为3或2；
故答案为：3或2．