题目内容
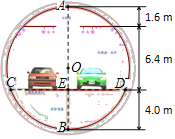
【题目】如图,矩形纸片![]() ,将
,将![]() 和
和![]() 分别沿
分别沿![]() 和
和![]() 折叠(
折叠(![]() ),点
),点![]() 和点
和点![]() 都与点
都与点![]() 重合;再将
重合;再将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在线段
落在线段![]() 上点
上点![]() 处.
处.
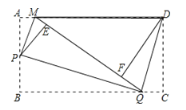
(1)判断![]() 和
和![]() 中有哪几对相似三角形? (不需说明理由)
中有哪几对相似三角形? (不需说明理由)
(2)如果![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() 与
与![]() 与
与![]() 与
与![]() 三对相似三角形;(2)
三对相似三角形;(2)![]() .
.
【解析】
(1)由矩形的性质得∠A=∠B=∠C=90°,由折叠的性质和等角的余角相等,可得∠BPQ=∠AMP=∠DQC,所以△AMP∽△BPQ∽△CQD;
(2)先证明MD=MQ,然后根据sin∠DMF![]() ,设DF=3x,MD=5x,表示出AP、BP、BQ,再根据△AMP∽△BPQ,列出比例式解方程求解即可.
,设DF=3x,MD=5x,表示出AP、BP、BQ,再根据△AMP∽△BPQ,列出比例式解方程求解即可.
解:(1)△AMP∽△BPQ∽△CQD,理由如下:
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,
根据折叠的性质可知:∠APM=∠EPM,∠EPQ=∠BPQ,
∴∠APM+∠BPQ=∠EPM+∠EPQ=90°,
∵∠APM+∠AMP=90°,
∴∠BPQ=∠AMP,
∴△AMP∽△BPQ,
同理:△BPQ∽△CQD,
根据相似的传递性,△AMP∽△CQD;
故![]() 与
与![]() 与
与![]() 与
与![]() 三对相似三角形;
三对相似三角形;
(2)∵AD∥BC,∴∠DQC=∠MDQ,
根据折叠的性质可知:∠DQC=∠DQM,
∴∠MDQ=∠DQM,∴MD=MQ,
∵AM=ME,BQ=EQ,∴BQ=MQ-ME=MD-AM,
∵sin∠DMF=![]() ,∴设DF=3x,MD=5x,
,∴设DF=3x,MD=5x,
∴BP=PA=PE=![]() ,BQ=5x-1,
,BQ=5x-1,
∵△AMP∽△BPQ,∴![]() ,
,
 ,
,
解得:x=![]() (舍)或x=2,
(舍)或x=2,
∴AB=3x=6.

练习册系列答案
相关题目