题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,动点P以
,动点P以![]() 的速度从A点出发,沿
的速度从A点出发,沿![]() 向C点移动,同时动点Q以
向C点移动,同时动点Q以![]() 的速度从点C出发,沿
的速度从点C出发,沿![]() 向点B移动,设P、Q两点移动的时间为t秒
向点B移动,设P、Q两点移动的时间为t秒![]() .
.

(1)t为多少时,以P、Q、C为顶点的三角形与![]() 相似?
相似?
(2)在P、Q两点移动过程中,四边形![]() 与
与![]() 的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
【答案】(1)t为![]() 或
或![]() 时,以P、Q、C为顶点的三角形与
时,以P、Q、C为顶点的三角形与![]() 相似;(2)四边形
相似;(2)四边形![]() 与
与![]() 的面积不能相等,理由见解析.
的面积不能相等,理由见解析.
【解析】
(1)先利用勾股定理计算出AC=10,由于∠PCQ=∠ACB,根据三角形相似的判定,当∠PQC=∠B时可判断CQP∽△CBA,利用相似比得到![]() ;当∠PQC=∠BAC时可判断△CQP∽△CAB,利用相似比得到
;当∠PQC=∠BAC时可判断△CQP∽△CAB,利用相似比得到![]() ,然后分别解方程求出t的值即可;
,然后分别解方程求出t的值即可;
(2)作PQ⊥BC于H,如图,先证明△CPH∽△CAB,利用相似比可得到PH=![]() ,再利用四边形ABQP与△CPQ的面积相等得到S△ABC=2S△CPQ,利用三角形面积公式得到2
,再利用四边形ABQP与△CPQ的面积相等得到S△ABC=2S△CPQ,利用三角形面积公式得到2![]() 68,然后解关于t的方程可判断四边形ABQP与△CPQ的面积能否相等.
68,然后解关于t的方程可判断四边形ABQP与△CPQ的面积能否相等.
(1)在R![]() 中,
中,![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() ,则
,则![]() ,即
,即![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,则
,则![]() ,即
,即![]() ,解得
,解得![]() ;
;
∴t为![]() 或
或![]() 时,以P、Q、C为顶点的三角形与
时,以P、Q、C为顶点的三角形与![]() 相似;
相似;
(2)四边形![]() 与
与![]() 的面积不能相等.
的面积不能相等.
理由如下:
作![]() 于H,如图,
于H,如图,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
当四边形![]() 与
与![]() 的面积相等时,
的面积相等时,
![]() ,即
,即![]() ,
,
∴![]() ,
,
整理得![]() ,此时方程无实数解,
,此时方程无实数解,
∴四边形![]() 与
与![]() 的面积不能相等.
的面积不能相等.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .
【题目】知抛物线y=x2﹣4x+2.
(1)此抛物线与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线.
x | … | … | |||||
y | … | … |
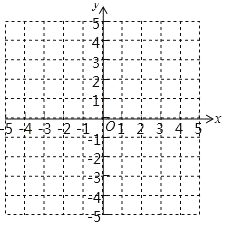
(3)结合图象回答:若点A(6,t)和点B(m,n)都在抛物线y=x2﹣4x+2上,且n<t,则m的取值范围是 .