题目内容
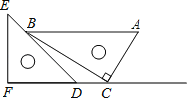
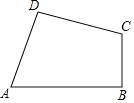
【题目】如图,在四边形ABCD中,AD=CD,AB﹣BC=2,∠B=∠D=90°.若四边形ABCD的面积为16,则AB的长为( )
A.3B.4C.5D.5![]()
【答案】C
【解析】
过点D作DE⊥AB于E,作CF⊥DE于F,则四边形BCFE为矩形得出BE=CF,BC=EF,易证∠DAE=∠CDF,由AAS证得△DAE≌△CDF,得出DE=CF,AE=DF,四边形ABCD的面积=2S△DAE+S矩形BCFE=CF2=16,得出BE=CF=4,求出AB﹣BC=2DF=2,则AE=DF=1,即可得出结果.
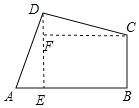
解:过点D作DE⊥AB于E,作CF⊥DE于F,如图所示:
则四边形BCFE为矩形,
∴BE=CF,BC=EF,
∵∠CDF+∠ADE=90°,∠ADE+∠DAE=90°,
∴∠DAE=∠CDF,
在△DAE和△CDF中,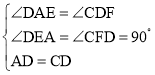 ,
,
∴△DAE≌△CDF(AAS),
∴DE=CF,AE=DF,
四边形ABCD的面积=2S△DAE+S矩形BCFE=2×![]() DEAE+CFEF=CFDF+CFEF=CF(DF+EF)=CF2=16,
DEAE+CFEF=CFDF+CFEF=CF(DF+EF)=CF2=16,
∴BE=CF=4,
AB﹣BC=AE+BE﹣BC=DF+DE﹣BC=DF+DF=2DF=2,
∴AE=DF=1,
∴AB=AE+BE=1+4=5,
故选:C.

 阅读快车系列答案
阅读快车系列答案【题目】已知一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 0 | p | m | 3 |
| q | 0 | … |
(1)求这个二次函数的表达式;
(2)表格中字母m= ;(直接写出答案)
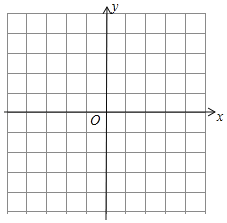
(3)在给定的直角坐标系中,画出这个二次函数的图象;
(4)以上二次函数的图象与x轴围成的封闭区域内(不包括边界),横、纵坐标都是整数的点共有 个.(直接写出结果)
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.