题目内容
【题目】已知二次函数y=ax2+bx+c的图象抛物线经过(﹣5，0)，(0，
)，(1，6)三点，直线L的解析式为y=2x﹣3
(1)求抛物线的函数解析式.
(2)求证：抛物线与直线L无公共点.
【答案】(1)y=
x2+3x+
；(2)证明见解析.
【解析】
（1）直接把点(﹣5，0)，(0，)，(1，6)代入二次函数y=ax2+bx+c，求出a、b、c的值即可；（2）把（1）中求出的抛物线的解析式与直线l的解析式y=2x-3组成方程组，再根据一元二次方程根的判别式即可得出结论；
(1)∵次函数y=ax2+bx+c的图象抛物线经过(﹣5，0)，(0，)，(1，6)三点，
∴
，
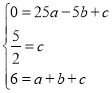解得
，
∴抛物线G的函数解析式为：y=x2+3x+；
(2)
，
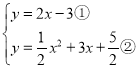①﹣②得，x2+x+
=0，
∵△=12﹣4××=﹣10＜0，
∴方程无实数根，即抛物线与直线L无公共点；
练习册系列答案
相关题目
【题目】有这样一个问题：探究函数y＝
的图象与性质.小美根据学习函数的经验，对函数y＝的图象与性质进行了探究下面是小美的探究过程，请补充完整：
(1)函数y＝的自变量x的取值范围是 ；
(2)下表是y与x的几组对应值.
x | －2 | － | －1 | － |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | － | －1 | － |
|
|
| m |
|
| … |
求m的值；
(3)如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点.根据描出的点，画出该函数的图象；
(4)结合函数的图象，写出该函数的一条性质： .
【题目】某学习小组在研究函数y=
x3﹣2x的图象与性质时，已列表、描点并画出了图象的一部分．
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
（1）请补全函数图象；
（2）方程
x3﹣2x=﹣2实数根的个数为 ；
（3）观察图象，写出该函数的两条性质．
