Question

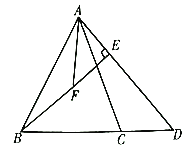
【题目】如图，在梯形中，，，点是的中点，与交于点，那么和的面积比是____．

Answer 1

【答案】

【解析】

延长BE，AD交于G，根据平行线的性质得到∠G=∠EBC，根据全等三角形的性质得到DG=BC=2AD，GE=BE，于是得到AG=3AD，通过△AGF∽△BCF，得到===，设GF=3x，BF=2x，求得=，由==，得到S△ABF=S△BCF，由==4，得到S△CEF=S△BCF，即可得到结论．

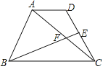
延长BE，AD交于G，

∵AD∥BC，

∴∠G=∠EBC，

在△DGE与△BCE中，

，

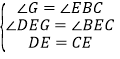∴△DGE≌△BCE，

∴DG=BC=2AD，GE=BE，

∴AG=3AD，

∵AD∥BC，

∴△AGF∽△BCF，

∴===，

∴设GF=3x，BF=2x，

∴BG=5x，

∴BE=GE=2.5x，

∴EF=12x，

∴=，

∴==，

∴S△ABF=S△BCF，

∵==4，

∴S△CEF=S△BCF，

∴△ABF和△CEF的面积比= =6:1.

故答案为：6:1.