题目内容
【题目】如图，已知
的斜边
，
．
以点
为圆心作圆，当半径为多长时，直线
与
相切？为什么？
以点为圆心，分别以
和
为半径作两个圆，这两个圆与直线分别有怎样的位置关系？
【答案】（1）以点
为圆心，当半径为
时，
与
相切；（2）以点为圆心，分别以
和
为半径作两个圆，这两个圆与直线分别相离和相交.
【解析】
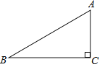
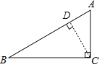
（1）过点C作CD垂直于AB，根据直线与圆相切时，圆心到直线的距离等于圆的半径，可得出圆C与AB相切时，CD为此时圆C的半径，在直角三角形ABC中，由AB及AC的长，利用勾股定理求出BC的长，由直角三角形的面积可以由斜边AB与高CD乘积的一半来，也可以由两直角边乘积的一半来求，可得出CD的长，即为AB与圆C相切时的半径；
（2）用半径和CD的长比较后即可得到结论．
解：
过作
，交于点
，如图所示：
的斜边
，
，
根据勾股定理得：
，
∵
，
∴
，
则以点为圆心，当半径为时，与相切；
∵
∴以点为圆心，分别以和为半径作两个圆，这两个圆与直线分别相离和相交；
练习册系列答案
相关题目
【题目】二次函数
，
，
是常数，且
中的
与
的部分对应值如下表所示，则下列结论中，正确的个数有（ ）
|
|
|
|
|
|
|
|
|
|
；
当
时，
；
当
时，的值随值的增大而减小；
方程
有两个不相等的实数根．
A. 4个 B. 3个 C. 2个 D. 1个
