题目内容
【题目】(问题情境)如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,我们可以利用
,我们可以利用![]() 与
与![]() 相似证明
相似证明![]() ,这个结论我们称之为射影定理,试证明这个定理;
,这个结论我们称之为射影定理,试证明这个定理;
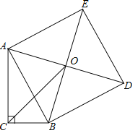
(结论运用)如图![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是对角线
是对角线![]() 、
、![]() 的交点,点
的交点,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
(1)试利用射影定理证明![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
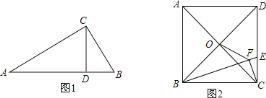
【答案】【问题情境】证明见解析;【结论运用】![]() 证明见解析;(2)
证明见解析;(2)![]() .
.
【解析】
通过证明Rt△ACD∽Rt△ABC得到AC:AB=AD:AC,然后利用比例性质即可得到AC2=ADAB;
【结论运用】
(1)根据射影定理得BC2=BOBD,BC2=BFBE,则BOBD=BFBE,即![]() =
=![]() ,加上∠OBF=∠EBD,于是可根据相似三角形的判定得到△BOF∽△BED;
,加上∠OBF=∠EBD,于是可根据相似三角形的判定得到△BOF∽△BED;
(2)先计算出DE=4,CE=2,BE=2![]() ,OB=3
,OB=3![]() ,再利用(1)中结论△BOF∽△BED得到
,再利用(1)中结论△BOF∽△BED得到![]() =
=![]() ,即
,即![]() =
=![]() ,然后利用比例性质求OF.
,然后利用比例性质求OF.
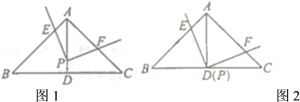
如图1.
∵CD⊥AB,∴∠ADC=90°,而∠CAD=∠BAC,∴Rt△ACD∽Rt△ABC,∴AC:AB=AD:AC,∴AC2=ADAB;
(1)如图2.
∵四边形ABCD为正方形,∴OC⊥BO,∠BCD=90°,∴BC2=BOBD.
∵CF⊥BE,∴BC2=BFBE,∴BOBD=BFBE,即![]() =
=![]() ,而∠OBF=∠EBD,∴△BOF∽△BED;
,而∠OBF=∠EBD,∴△BOF∽△BED;
(2)∵BC=CD=6,而DE=CE,∴DE=4,CE=2.
在Rt△BCE中,BE=![]() =2
=2![]() .在Rt△OBC中,OB=
.在Rt△OBC中,OB=![]() BC=3
BC=3![]() .
.
∵△BOF∽△BED,∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴OF=
,∴OF=![]() .
.

练习册系列答案
相关题目
【题目】二次函数![]() ,
,![]() ,
,![]() 是常数,且
是常数,且![]() 中的
中的![]() 与
与![]() 的部分对应值如下表所示,则下列结论中,正确的个数有( )
的部分对应值如下表所示,则下列结论中,正确的个数有( )
|
|
|
|
|
|
|
|
|
|
![]() ;
;![]() 当
当![]() 时,
时,![]() ;
;![]() 当
当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;
值的增大而减小;
![]() 方程
方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个