题目内容
【题目】课上教师呈现一个问题

甲、乙、丙三位同学用不同的方法添加辅助线解决问题,如下图:
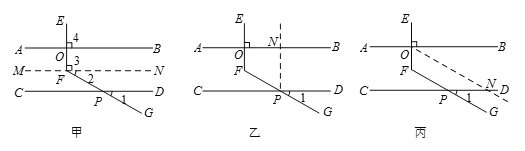
甲同学辅助线的做法和分析思路如下:

(1)请你根据乙同学所画的图形,描述辅助线的做法,并写出相应的分析思路.
辅助线:___________________;
分析思路:
(2)请你根据丙同学所画的图形,求∠EFG的度数.
【答案】(1)辅助线:过点P作PN∥EF交AB于点N.
分析思路:
①欲求∠EFG的度数,由辅助线作图可知,∠EFG=∠NPG,
因此,只需转化为求∠NPG的度数;
②欲求∠NPG的度数,由图可知只需转化为求∠1和∠2的度数;
③又已知∠1的度数,所以只需求出∠2的度数;
④由已知EF⊥AB,可得∠4=90°;
⑤由PN∥EF,可推出∠3=∠4;AB∥CD可推出∠2=∠3,由此可推∠2=∠4,
所以可得∠2的度数;
⑥从而可以求出∠EFG的度数.
(2)120°
【解析】(1)辅助线:过点P作PN∥EF交AB于点N.
分析思路:
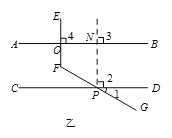
①欲求∠EFG的度数,由辅助线作图可知,∠EFG=∠NPG,
因此,只需转化为求∠NPG的度数;
②欲求∠NPG的度数,由图可知只需转化为求∠1和∠2的度数;
③又已知∠1的度数,所以只需求出∠2的度数;
④由已知EF⊥AB,可得∠4=90°;
⑤由PN∥EF,可推出∠3=∠4;AB∥CD可推出∠2=∠3,由此可推∠2=∠4,
所以可得∠2的度数;
⑥从而可以求出∠EFG的度数.
(2)过点O作ON∥FG
∵ON∥FG
∴∠EFG=∠EON ∠1=∠ONC=30°
∵AB∥CD
∴∠ONC=∠BON=30°
∵EF⊥AB
∴∠EOB=90°
∴∠EFG=∠EON=∠EOB+∠BON=90°+30°=120°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目