题目内容
如图1,在平面直角坐标系中,正方形OABC的顶点A(﹣6,0),过点E(﹣2,0)作EF∥AB,交BO于F;

(1)求EF的长;
(2)过点F作直线l分别与直线AO、直线BC交于点H、G;
①根据上述语句,在图1上画出图形,并证明 ;
;
②过点G作直线GD∥AB,交x轴于点D,以圆O为圆心,OH长为半径在x轴上方作半圆(包括直径两端点),使它与GD有公共点P.如图2所示,当直线l绕点F旋转时,点P也随之运动,证明: ,并通过操作、观察,直接写出BG长度的取值范围(不必说理);
,并通过操作、观察,直接写出BG长度的取值范围(不必说理);
(3)在(2)中,若点M(2, ),探索2PO+PM的最小值.
),探索2PO+PM的最小值.

(1)求EF的长;
(2)过点F作直线l分别与直线AO、直线BC交于点H、G;
①根据上述语句,在图1上画出图形,并证明
 ;
;②过点G作直线GD∥AB,交x轴于点D,以圆O为圆心,OH长为半径在x轴上方作半圆(包括直径两端点),使它与GD有公共点P.如图2所示,当直线l绕点F旋转时,点P也随之运动,证明:
 ,并通过操作、观察,直接写出BG长度的取值范围(不必说理);
,并通过操作、观察,直接写出BG长度的取值范围(不必说理);(3)在(2)中,若点M(2,
 ),探索2PO+PM的最小值.
),探索2PO+PM的最小值.(1)2
(2)①见解析 ②见解析
(3)8
(2)①见解析 ②见解析
(3)8
试题分析:(1)利用正方形与平行线的性质,易求线段EF的长度.
(2)①首先依题意画出图形,如答图1所示.证明△OFH∽△BFG,得
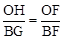 ;由EF∥AB,得
;由EF∥AB,得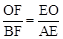 .所以
.所以 。
。②由OP=OH,则问题转化为证明
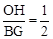 ,根据①中的结论,易得
,根据①中的结论,易得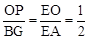 ,故问题得证。
,故问题得证。(3)本问为探究型问题,利用线段性质(两点之间线段最短)解决,如答图2所示,构造矩形,将2PO+PM转化为NK+PM,由NK+PM≥NK+KM,NK+KM≥MN=8,可得当点P在线段MN上时,2OP+PM的值最小,最小值为8。
解:(1)在正方形OABC中,∠FOE=∠BOA=
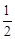 ∠COA=45°。
∠COA=45°。∵EF∥AB,∴∠FEO=∠BAO=90°。∴∠EFO=∠FOE=45°。
又E(﹣2,0),∴EF=EO=2。
(2)①画图,如答图1所示。
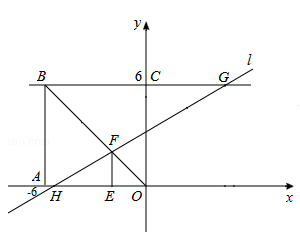
证明:∵四边形OABC是正方形,∴OH∥BC。
∴△OFH∽△BFG。∴
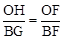 。
。∵EF∥AB,∴
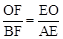 。
。∴
 。
。②证明:∵半圆与GD交于点P,∴OP=OH。
由①得:
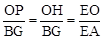 ,
,又EO=2,EA=OA﹣EO=6﹣2=4,
∴
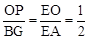 。
。通过操作、观察可得,4≤BG≤12。
(3)由(2)可得:
 ,
,∴2OP+PM=BG+PM。
如答图2所示,过点M作直线MN⊥AB于点N,交GD于点K,则四边形BNKG为矩形。
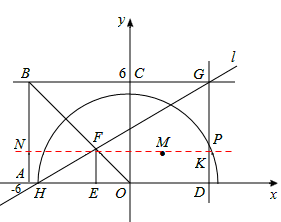
∴NK=BG。
∴2OP+PM=BG+PM=NK+PM≥NK+KM,当点P与点K重合,即当点P在直线MN上时,等号成立。
又∵NK+KM≥MN=8,当点K在线段MN上时,等号成立。
∴当点P在线段MN上时,2OP+PM的值最小,最小值为8。

练习册系列答案
相关题目
 ,0)、B(0,4),对△OAB连续作旋转变换,
,0)、B(0,4),对△OAB连续作旋转变换,