��Ŀ����
����Ŀ����ͼ1����֪��MON=140�㣬��AOC���BOC���࣬OCƽ�֡�MOB��
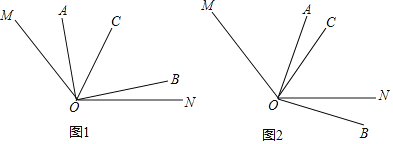
��1����ͼ1�У�����AOC=40�������BOC= �㣬��NOB= �㣮
��2����ͼ1�У����AOC=������NOB=������̽��������֮���������ϵ�� ����д����������Ҫ���̣���ÿһ�����治��д�����ɣ���
��3������֪���������ǰ���£�����AOB���ŵ�O˳ʱ��ת������ͼ2��λ�ã���ʱ������֮���������ϵ�Ƿ���������������˵�����ɣ�������������ֱ��д����ʱ������֮���������ϵ��
���𰸡��⣺��1��50��40����2����=2����40��;��3������������ʱ��ʱ������֮���������ϵΪ��2��+��=40��.
��������
��1���ȸ�����ǵĶ�������BOC=50�������ɽ�ƽ���ߵĶ�������BOM=100�������ݽǵIJ�ɵá�BON�Ķ�����
��2��ͬ���ȼ����MOB=2��BOC=2��90��-����=180��-2�����ٸ��ݡ�BON=��MON-��BOM�е�ʽ���ɣ�
��3��ͬ���ɵá�MOB=180��-2�����ٸ��ݡ�BON+��MON=��BOM�е�ʽ���ɣ�
��1����ͼ1��
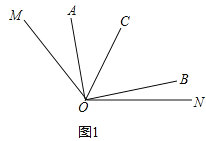
�ߡ�AOC���BOC���࣬
���AOC+��BOC=90����
�ߡ�AOC=40����
���BOC=50����
��OCƽ�֡�MOB��
���MOC=��BOC=50����
���BOM=100����
�ߡ�MON=40����
���BON=��MON-��BOM=140��-100��=40����
��2����=2��-40���������ǣ�
��ͼ1���ߡ�AOC=����
���BOC=90��-����
��OCƽ�֡�MOB��
���MOB=2��BOC=2��90��-����=180��-2����
�֡ߡ�MON=��BOM+��BON��
��140��=180��-2��+��������=2��-40�㣻
��3������������ʱ��ʱ������֮���������ϵΪ��2��+��=40�㣬
�����ǣ���ͼ2��
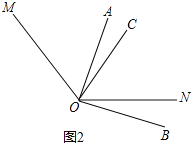
�ߡ�AOC=������NOB=����
���BOC=90��-����
��OCƽ�֡�MOB��
���MOB=2��BOC=2��90��-����=180��-2����
�ߡ�BOM=��MON+��BON��
��180��-2��=140��+������2��+��=40�㣬
�𣺲���������ʱ��ʱ������֮���������ϵΪ��2��+��=40.