Question

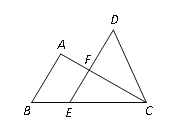
【题目】如图①，C地位于A、B两地之间，甲步行直接从C地前往B地，乙骑自行车由C地先回A地，再从A地前往B地（在A地停留时间忽略不计），已知两人同时出发且速度不变，乙的速度是甲的2.5倍，设出发xmin后，甲、乙两人离C地的距离为y1m、y2m，图②中线段OM表示y1与x的函数图象．

（1）甲的速度为______m/min．乙的速度为______m/min．

（2）在图②中画出y2与x的函数图象，并求出乙从A地前往B地时y2与x的函数关系式．

（3）求出甲、乙两人相遇的时间．

（4）请你重新设计题干中乙骑车的条件，使甲、乙两人恰好同时到达B地．

要求：①不改变甲的任何条件．

②乙的骑行路线仍然为从C地到A地再到B地．

③简要说明理由．

④写出一种方案即可．

Answer 1

【答案】（1）80；200；（2）画图如图②见解析；当乙由A到C时，4.5≤x≤9，y2=1800-200x，当乙由C到B时，9≤x≤21，y2=200x-1800；（3）甲、乙两人相遇的时间为第15min；（4）甲、乙同时到达A．

【解析】

（1）由图象求出甲的速度，再由条件求乙的速度；

（2）由乙的速度计算出乙到达A、返回到C和到达B所用的时间，图象可知，应用方程思想列出函数关系式；

（3）根据题意，甲乙相遇时，乙与甲的路程差为1800，列方程即可．

（4）由甲到B的时间，反推乙到达B所用时间也要为30min，则由路程计算乙所需速度即可．

解：（1）根据y1与x的图象可知，

甲的速度为，

则乙的速度为2.5×80=200m/min

故答案为：80，200

（2）根据题意画图如图②

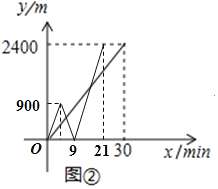
当乙由A到C时，4.5≤x≤9

y2=900-200（x-4.5）=1800-200x

当乙由C到B时，9≤x≤21

y2=200（x-9）=200x-1800

（3）由已知，两人相遇点在CB之间，

则200x-80x=2×900

解得x=15

∴甲、乙两人相遇的时间为第15min．

（4）改变乙的骑车速度为140m/min，其它条件不变

此时甲到B用时30min，乙的用时为min

则甲、乙同时到达A．