题目内容
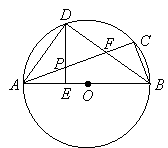
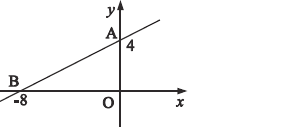
【题目】如图,直线![]() 与坐标轴交于点
与坐标轴交于点![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积为
的面积为![]() .
.

(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析式;
的解析式;
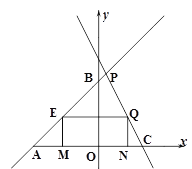
(3)若点![]() 是线段
是线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,
,![]() 轴,
轴,![]() 轴,垂足分别为点
轴,垂足分别为点![]() 、
、![]() ,是否存在点
,是否存在点![]() ,使得四边形
,使得四边形![]() 为正方形,若存在,请求出点
为正方形,若存在,请求出点![]() 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.
【答案】(1)![]() ,
,![]() 点为
点为![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 点为
点为![]() ,理由见解析
,理由见解析
【解析】
(1)利用一次函数图象上点的坐标特征可求出m的值及点A的坐标;
(2)过点P作PH⊥x轴,垂足为H,则PH=![]() ,利用三角形的面积公式结合△PAC的面积为
,利用三角形的面积公式结合△PAC的面积为![]() ,可求出AC的长,进而可得出点C的坐标,再根据点P,C的坐标,利用待定系数法即可求出直线PC的解析式;
,可求出AC的长,进而可得出点C的坐标,再根据点P,C的坐标,利用待定系数法即可求出直线PC的解析式;
(3)由题意,可知:四边形EMNQ为矩形,设点E的纵坐标为t,利用一次函数图象上点的坐标特征可得出点E的坐标为(t-3,t)、点Q的坐标为(![]() ,t),利用正方形的性质可得出关于t的一元一次方程,解之即可得出结论.
,t),利用正方形的性质可得出关于t的一元一次方程,解之即可得出结论.
解:(1)把点![]() 代入直线
代入直线![]() ,
,
即 ![]() 时,
时,![]()
直线![]() ,当
,当![]() 时,
时,![]() 得:
得:![]()
![]() ,
,![]() 点为
点为![]()
(2)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,由(1)得,
,由(1)得,![]()
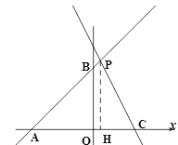
∴ ![]()
![]()
解得:![]()
![]()
![]() 点
点![]() 为
为![]()
设直线![]() 为
为![]() ,把点
,把点![]() 、
、![]() 代入,得:
代入,得:
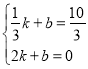 解得:
解得:![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
(3)由已知可得,四边形![]() 为矩形,
为矩形,
设点![]() 的纵坐标为
的纵坐标为![]() ,则
,则![]() 得:
得: ![]()
![]() 点为
点为![]()
![]() 轴
轴
![]() 点的纵坐标也为
点的纵坐标也为![]()
![]() 点在直线
点在直线![]() 上,当
上,当![]() 时,
时,![]()
![]()
![]()
又![]()
当![]() 时,矩形
时,矩形![]() 为正方形,所以
为正方形,所以![]()
![]()
故![]() 点为
点为![]()

【题目】下表是某校七~九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,文艺小组每次活动时间比科技小组每次活动时间多0.5小时.设文艺小组每次活动时间为![]() 小时,请根据表中信息完成下列解答.
小时,请根据表中信息完成下列解答.
课外小组活动 总时间(小时) | 文艺小组 活动次数 | 科技小组 活动次数 | |
七年级 | 12.5 | 4 | 3 |
八年级 | 10.5 | 3 |
|
九年级 | 7 |
|
|
(1)科技小组每次活动时间为______小时(用含![]() 的式子表示);
的式子表示);
(2)求八年级科技小组活动次数![]() 的值;
的值;
(3)直接写出![]() ______,
______,![]() ______.
______.