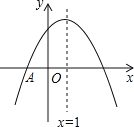��Ŀ����
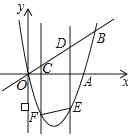
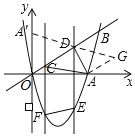
����Ŀ����ͼ�����κ���y=x2��4x��ͼ����x�ᡢֱ��y=x��һ������ֱ�Ϊ��A��B��CD���߶�OB�ϵ�һ���߶Σ���CD=2������C��D����ֱ�߶�ƽ����y�ᣬ���������ཻ�ڵ�F��E������EF��
��1����A������Ϊ�� �����߶�OB�ij�=�� ����
��2�����C�ĺ�����Ϊm��
�����ı���CDEF��ƽ���ı���ʱ����m��ֵ��
������AC��AD����mΪ��ֵʱ����ACD���ܳ���С������������Сֵ��
���𰸡���1�� A��4��0����5![]() ����2����
����2����![]() ���ڵ�m=
���ڵ�m=![]() ʱ����ACD���ܳ���С�������СֵΪ8��
ʱ����ACD���ܳ���С�������СֵΪ8��
��������
��1������y=x2��4x�У���y=0����0=x2��4x�������A��4��0�����ⷽ����![]() ���ɵ�B��5��5���������ó�OB�ij���
���ɵ�B��5��5���������ó�OB�ij���
��2���ٸ���C��m��m����F��m��m2��4m�����ɵ�CF=m����m2��4m��������D��m![]() ��m
��m![]() ����E��m
����E��m![]() ����m
����m![]() ��2��4��m
��2��4��m![]() �������ɵ�DE=m
�������ɵ�DE=m![]() [��m
[��m![]() ��2��4��m
��2��4��m![]() ��]�������ݵ��ı���CDEF��ƽ���ı���ʱ��CF=DE�����m��ֵ���ɣ�
��]�������ݵ��ı���CDEF��ƽ���ı���ʱ��CF=DE�����m��ֵ���ɣ�
���ȹ���A��CD��ƽ���ߣ�����D��AC��ƽ���ߣ����ڵ�G�����ı���ACDG��ƽ���ı��Σ��ó�AC=DG��������A����ֱ��OB�ĶԳƵ�A'������A'D����A'D=AD�����ݵ�A'��D��G���㹲��ʱ��A'D+DG=A'G��̣��ɵô�ʱAC+AD��̣�Ȼ�����ֱ��A'G�Ľ���ʽΪy![]() x+4���ⷽ����ɵ�D��C�����꣬�������������빫ʽ����á�ACD���ܳ�����Сֵ��
x+4���ⷽ����ɵ�D��C�����꣬�������������빫ʽ����á�ACD���ܳ�����Сֵ��
��1����y=x2��4x����y=0����0=x2��4x��
��ã�x1=0��x2=4��
��A��4��0�����ⷽ����![]() ��
��
�ɵã�![]() ��
��![]() ��
��
��B��5��5����
��OB![]() ��
��
�ʴ�Ϊ����4��0����5![]() ��
��
��2���١ߵ�C�ĺ�����Ϊm����CF��DE��y�ᣬ
��C��m��m����F��m��m2��4m����
�֡�CD=2����CD���߶�OB�ϵ�һ���߶Σ�
��D��m![]() ��m
��m![]() ����E��m
����E��m![]() ����m
����m![]() ��2��4��m
��2��4��m![]() ������
������
��CF=m����m2��4m����DE=m![]() [��m
[��m![]() ��2��4��m
��2��4��m![]() ��]��
��]��
�ߵ��ı���CDEF��ƽ���ı���ʱ��CF=DE��
��m����m2��4m��=m![]() [��m
[��m![]() ��2��4��m
��2��4��m![]() ��]��
��]��
��ã�![]() ��
��
����ͼ��ʾ������A��CD��ƽ���ߣ�����D��AC��ƽ���ߣ����ڵ�G�����ı���ACDG��ƽ���ı��Σ�
��AC=DG��
����A����ֱ��OB�ĶԳƵ�A'������A'D����A'D=AD��
�൱A'��D��G���㹲��ʱ��A'D+DG=A'G��̣���ʱAC+AD��̣�
��A��4��0����AG=CD=2��
��A'��0��4����G��4![]() ����
����
��ֱ��A'G�Ľ���ʽΪy=kx+b����![]() ��
��
��ã�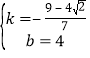 ��
��
��ֱ��A'G�Ľ���ʽΪy![]() x+4��
x+4��
�ⷽ����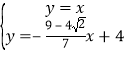 ��
��
�ɵã�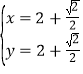 ��
��
��D��![]() ��
��![]() ����
����
��CD=2����CD���߶�OB�ϵ�һ���߶Σ�
��C��![]() ��
��![]() ����
����
���C�����m=![]() ��
��
��AD=A'D��AC=DG��CD=AG=2��
���ACD����СֵΪA'G+AG=![]() =6+2=8��
=6+2=8��
�ʵ�m=![]() ʱ����ACD���ܳ���С�������СֵΪ8��
ʱ����ACD���ܳ���С�������СֵΪ8��

 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�