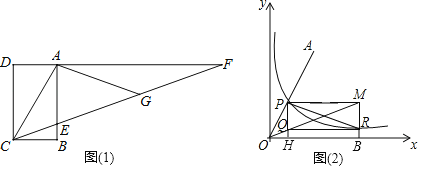
题目内容
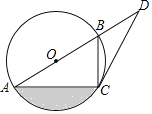
【题目】如图,点![]() 在正方形
在正方形![]() 的边
的边![]() 上,连接
上,连接![]() ,设点
,设点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,且点
,且点![]() 在正方形内部,连接
在正方形内部,连接![]() 并延长交边
并延长交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,则
,则![]() 的长为__________.
的长为__________.
【答案】![]()
【解析】
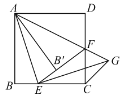
根据对称得:△ABE≌△AB'E,再由HL证明Rt△AB'F≌Rt△ADF,即可得B'F=DF,如图,作辅助线,构建BM=BE,先证明∠EAF=45°,得AE=EG,证明△AME≌△ECG,则EM=CG,根据等腰直角的性质得:EM=![]() BE,即可得出结论.
BE,即可得出结论.
解:如图,在线段AB上截取BM,使BM=BE,连接ME,
∵四边形ABCD是正方形,
∴AD=AB,∠B=∠D=90°,
∵点B关于直线AE的对称点为B',
∴△ABE≌△AB'E,
∴∠BAE=∠B'AE,AB=AB'=AD,∠AB'E=∠B=90°,
∴∠AB' F=90°,
在Rt△AB'F和Rt△ADF中,
∵![]() ,
,
∴Rt△AB'F≌Rt△ADF(HL),
∴∠DAF=∠B'AF,
∵AB=BC,BM=BE,
∴AM=EC,
∵∠BAE=∠B'AE,∠DAF=∠B'AF,
又∵∠BAD=90°,
∴2∠B'AE +2∠B'AF=90°,
∴∠B'AE +∠B'AF=45°,
即∠EAF=45°,
∵AE⊥EG,
∴∠AEG=90°,
∴△AEG是等腰直角三角形,
∴∠AEB+∠CEG=∠AEB+∠BAE=90°,AE=EG,
∴∠BAE=∠CEG,
在△AME和△ECG中,
∵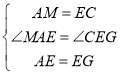 ,
,
∴△AME≌△ECG(SAS),
∴EM=CG,
Rt△BEM中,∠B=90°,BM=BE,
∴EM=![]() BE,
BE,
∴CG=![]() BE,
BE,
∵![]() ,
,
∴CG=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目