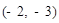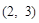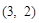题目内容
如图,直线l经过点A(1,0),且与曲线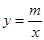 (x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线
(x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线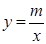 (x>0)和
(x>0)和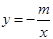 (x<0)于M,N两点.
(x<0)于M,N两点.

小题1:求m的值及直线l的解析式;
小题2:是否存在实数p,使得S△AMN=4S△APM?若存在,请求出所有满足条件的p的值;若不存在,请说明理由
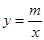 (x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线
(x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线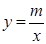 (x>0)和
(x>0)和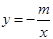 (x<0)于M,N两点.
(x<0)于M,N两点.
小题1:求m的值及直线l的解析式;
小题2:是否存在实数p,使得S△AMN=4S△APM?若存在,请求出所有满足条件的p的值;若不存在,请说明理由
小题1:m=2时直线l的解析式是y=x-1。
小题2:见解析。
解:(1)把B(2,1)代入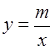 (x>0)中,可得m=2.--------1分
(x>0)中,可得m=2.--------1分
设直线l的解析式是y=kx+b,
把A(1,0),B(2,1)代入y=kx+b中,得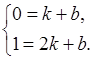 --------3分
--------3分
解得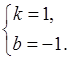 ∴直线l的解析式是y=x-1.-------5分
∴直线l的解析式是y=x-1.-------5分
(2)由P(p,p-1),可知点P在直线l上,且得
M(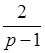 ,p-1),N(-
,p-1),N(-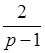 ,p-1),--------2分
,p-1),--------2分
∴MN=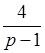 .∴S△AMN=
.∴S△AMN=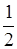 ·
·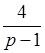 ·(p-1)=2.--------4分
·(p-1)=2.--------4分
6 p-1=1,即p=2时,P与B重合,△APM不存在.--------5分
②当p>2时(如图①),
S△APM =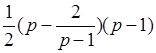 =
=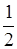 (p2-p-2).
(p2-p-2).
由S△AMN =4S△APM,得4·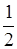 (p2-p-2)=2.---------------6分
(p2-p-2)=2.---------------6分
解得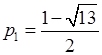 (不合题意,舍去),
(不合题意,舍去),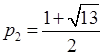 .
.
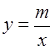 (x>0)中,可得m=2.--------1分
(x>0)中,可得m=2.--------1分设直线l的解析式是y=kx+b,
把A(1,0),B(2,1)代入y=kx+b中,得
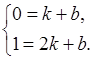 --------3分
--------3分解得
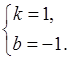 ∴直线l的解析式是y=x-1.-------5分
∴直线l的解析式是y=x-1.-------5分(2)由P(p,p-1),可知点P在直线l上,且得
M(
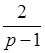 ,p-1),N(-
,p-1),N(-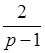 ,p-1),--------2分
,p-1),--------2分∴MN=
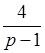 .∴S△AMN=
.∴S△AMN=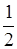 ·
·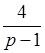 ·(p-1)=2.--------4分
·(p-1)=2.--------4分6 p-1=1,即p=2时,P与B重合,△APM不存在.--------5分
②当p>2时(如图①),
S△APM =
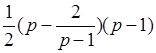 =
=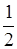 (p2-p-2).
(p2-p-2).由S△AMN =4S△APM,得4·
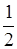 (p2-p-2)=2.---------------6分
(p2-p-2)=2.---------------6分解得
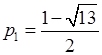 (不合题意,舍去),
(不合题意,舍去),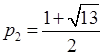 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
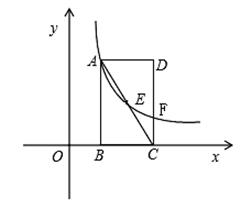
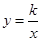 的图象经过直线AC上的点E,且点E的坐标为(2,m),求
的图象经过直线AC上的点E,且点E的坐标为(2,m),求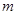 的值及反比例函数的解析式;
的值及反比例函数的解析式;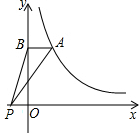
 、
、 在第一象限的图像如图,
在第一象限的图像如图, ,过
,过 ,作
,作 轴的平行线交
轴的平行线交 , 交
, 交 轴于
轴于 ,若
,若 ,则
,则
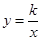 (x>0),则点B的坐标不可能的是( ▲ )
(x>0),则点B的坐标不可能的是( ▲ )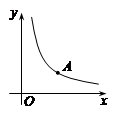
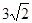 ,
,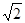 )
)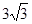 ,
,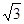 )
)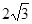 )
)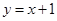 的图象与反比例函数
的图象与反比例函数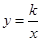 的图象在第一象限相交于点
的图象在第一象限相交于点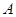 ,与
,与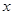 轴相交于点
轴相交于点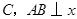 轴于点
轴于点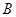 ,
, 的面积为1,则
的面积为1,则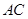 的长为 (保留根号).
的长为 (保留根号).
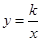 与直线
与直线 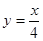 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线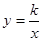 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线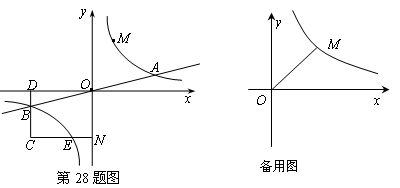
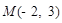 在双曲线
在双曲线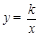 上,则下列各点一定在该双曲线上的是( )
上,则下列各点一定在该双曲线上的是( )