题目内容
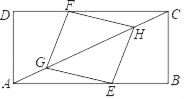
【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.
【答案】(1)见解析;(2)5.
【解析】
(1)依据矩形的性质,即可得出△AEG≌△CFH,进而得到GE=FH,∠CHF=∠AGE,由∠FHG=∠EGH,可得FH∥GE,即可得到四边形EGFH是平行四边形;
(2)由菱形的性质,即可得到EF垂直平分AC,进而得出AF=CF=AE,设AE=x,则FC=AF=x,DF=8-x,依据Rt△ADF中,AD2+DF2=AF2,即可得到方程,即可得到AE的长.
(1)证明:
![]() ,
,
![]()
![]()
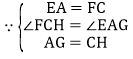 ,
,
![]()
![]() ,
,
![]()
![]()
(2)![]()
![]()
![]()
![]()
![]()
![]()
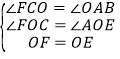
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
故答案为5.

练习册系列答案
相关题目
【题目】智能折叠电动车是在传统电动车的基础上,根据消费者需求生产的一种新型电动车.某智能折叠电动车公司计划每周生产1400辆,平均每天生产200辆.由于各种原因实际每天生产量与计划每天生产量相比有出入.下表是某周智能折叠电动车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆)

星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
生产情况 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产智能折叠电动车_______辆;
(2)产量最多的一天比产量最少的一天多生产________辆;
(3)若该公司实行按生产的智能折叠电动车数量的多少计工资,即计件工资制.如果每生产一辆智能折叠电动车可得人民币60元,那么该公司工人这一周的工资总额是多少元?