题目内容
【题目】如图所示，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（-2，0）、B（1，0），直线x= 
与此抛物线交于点C，与x轴交于点M，在直线上取点D，使MD=MC，连接AC，BC，AD，BD，某同学根据图象写出下列结论：①a-b=0；②当x＜ 时，y随x增大而增大；③四边形ACBD是菱形；④9a-3b+c＞0．你认为其中正确的是( )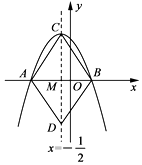
A.②③④
B.①②③
C.①③④
D.①②③④
【答案】B
【解析】（1）∵抛物线y=ax2+bx+c（a≠0）与x轴交于点A（-2，0）、B（1，0），
∴ 
①， 
②，
∴由①-②可得： 
，即： 
；故第一个结论正确；
（ 2 ）∵点A、B的坐标分别为（-2，0）、（1，0），点M的坐标为（-0.5，0），
∴点M是线段AB的中点，
∴直线 
是抛物线的对称轴，
又∵抛物线开口向下，
∴当x＜ 
时，y随x增大而增大，故第二个结论是正确的；
（ 3 ）∵点M既是AB中点，又是CD中点，且CD⊥AB，
∴CD与AB互相垂直平分，
∴四边形ACBD是菱形.故第三个结论是正确的；
（ 4 ）∵抛物线的开口向下，点A的坐标是（-2，0），
∴结合图象可知：当 
， 
，故第四个结论是错误的；
综上所述，正确的结论是①②③.
故答案为：B.
①由抛物线与x轴的两交点坐标即可得出抛物线的对称轴为x=-
=-0.5，由此即可得出a=b，或将A、B两点坐标分别代入函数解析式，建立方程组，利用加减消元法消去c，即可得出结果，①正确；
②根据抛物线的开口向下以及抛物线与x轴的两交点坐标，即可得出当-2<x<1时，y>0，②正确；
③由AB关于x=0.5对称，即可得出AM=BM，再结合MC=MD以及CD⊥AB，得出CD与AB互相垂直平分，即可得出四边形ACBD是菱形，③正确；
④根据当x=-3时，y<0，即可得出9a-3b+c<0，④错误。综上即可得出结论。
