题目内容
【题目】在平面直角坐标系中,点A,B分别是x轴正半轴与y轴正半轴上一点,OA=m,OB=n,以AB为边在第一象限内作正方形ABCD.
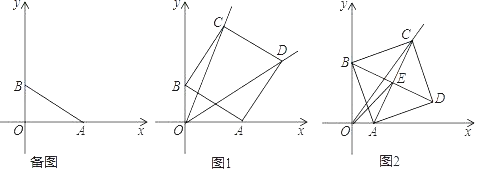
(1)若m=4,n=3,直接写出点C与点D的坐标;
(2)点C在直线y=kx(k>1且k为常数)上运动.
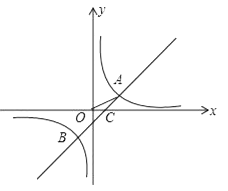
①如图1,若k=2,求直线OD的解析式;
②如图2,连接AC、BD交于点E,连接OE,若OE=2![]() OA,求k的值.
OA,求k的值.
【答案】(1)C(3,7),D(7,4);(2)①y=![]() x;②
x;②![]() .
.
【解析】
(1)根据题意把m=4,n=3代入解答即可;
(2)①利用待定系数法确定函数关系式即可;
②根据B、D坐标表示出E点坐标,由勾股定理可得到m、n之间的关系式,用m表示出C点坐标,根据函数关系式解答即可.
解:(1)∵OA=m,OB=n,以AB为边在第一象限内作正方形ABCD,
∴C(n,m+n),D(m+n,m),
把m=4,n=3代入可得:
C(3,7),D(7,4),
(2)①设C(a,2a),由题意可得:![]() ,
,
解得:m=n=a,
∴D(2a,a),
∴直线OD的解析式为:y=![]() x,
x,
②由B(0,n),D(m+n,m),
可得:E(![]() ,
,![]() ),OE=
),OE=![]() OA,
OA,
∴(![]() )2+(
)2+(![]() )2=8m2,
)2=8m2,
可得:(m+n)2=16m2,
∴m+n=4m,n=3n,
∴C(3m,4m),
∴直线OC的解析式为:y=![]() x,
x,
可得:k=![]() .
.
故答案为:(1)C(3,7),D(7,4);(2)①y=![]() x;②
x;②![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目