题目内容
【题目】学校为奖励在家自主学习有突出表现的学生,决定购买笔记本和钢笔作为奖品.已知1本笔记本和4支钢笔共需100元,4本笔记本和6支钢笔共需190元.
(1)分别求一本笔记本和一支钢笔的售价;
(2)若学校准备购进这两种奖品共90份,并且笔记本的数量不多于钢笔数量的3倍,请设计出最省钱的购买方案,并说明理由.
【答案】(1)一本笔记本的售价为16元,一支钢笔的售价为21元.(2)当购进67本笔记本、23支钢笔时,购买的总价最少,最少费用为1555元.
【解析】
(1)由题意分别设笔记本和钢笔的售价,列二元一次方程组即可求解.
(2)根据题意设购进m本笔记本,则购进(90﹣m)支钢笔,列不等式求出m取值范围,再列出学校购进这两种奖品的总价为w元,则w=16m+21(90﹣m)=﹣5m+1890.代入即可得出相应方案方案.
解:(1)设一本笔记本的售价为x元,一支钢笔的售价为y元,
依题意,得:![]() ,
,
解得:![]() .
.
答:一本笔记本的售价为16元,一支钢笔的售价为21元.
(2)设购进m本笔记本,则购进(90﹣m)支钢笔,
依题意,得:m≤3(90﹣m),
解得:m≤67![]() .
.
设学校购进这两种奖品的总价为w元,则w=16m+21(90﹣m)=﹣5m+1890.
∵﹣5<0,
∴w值随m值的增大而减小,
又∵m≤67![]() ,且m为整数,
,且m为整数,
∴当m=67时,w取得最小值,最小值为1555,
∴当购进67本笔记本、23支钢笔时,购买的总价最少,最少费用为1555元.

 名校课堂系列答案
名校课堂系列答案【题目】某校为了解中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
节目 | 人数(名) | 百分比 |
最强大脑 |
|
|
朗读者 |
|
|
中国诗词大会 |
|
|
出彩中国人 |
|
|
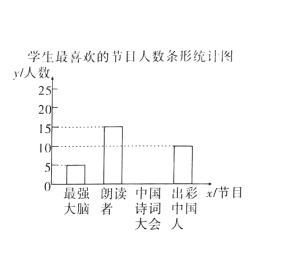
根据以上提供的信息.解答下列问题:
![]() ,
,![]() ,
,![]() ;
;
![]() 补全上面的条形统计图;
补全上面的条形统计图;
![]() 名女同学.其余为男同学,现要从中随机抽取
名女同学.其余为男同学,现要从中随机抽取![]() 名同学代表学校参加市里组织的竞赛活动,请求出所抽取的
名同学代表学校参加市里组织的竞赛活动,请求出所抽取的![]() 名同学恰好是
名同学恰好是![]() 名男同学和
名男同学和![]() 名女同学的概率.
名女同学的概率.