Question

【题目】已知是的边上一点，连结，此时有结论，请解答下列问题：

（1）当是边上的中点时，的面积 的面积（填“>”“<”或“=”）．

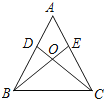
（2）如图1，点分别为边上的点，连结交于点，若、、的面积分别为5，8，10，则的面积是 （直接写出结论）．

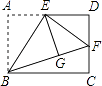
（3）如图2，若点分别是的边上的中点，且，求四边形的面积．可以用如下方法：连结，由得，同理：，设，，则，，由题意得，，可列方程组为：，解得，可得四边形的面积为20．解答下面问题：

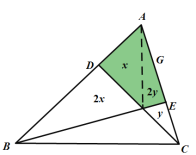
如图3，是的三等分点，是的三等分点，与交于，且，请计算四边形的面积，并说明理由．

图1 图2 图3

Answer 1

【答案】（1）=；（2）18；（3），见解析

【解析】

（1）利用同高（或同底）的三角形面积比等于对应边（或高）的比即可得．

（2）联结 ，利用同高的三角形面积比等于对应边的比，结合已知条件联立方程可得．

（3）联结 ，利用同高的三角形面积比等于对应边的比，结合已知条件联立方程可得．

（1）∵，是边上的中点

∴ ，则

（2）如图，连结

∵、、的面积分别为5，8，10，

∴，

∴

设，

则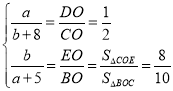

整理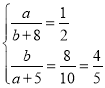得 解得，

则．

（3）连结，设，，

∴，，

∵，

∴

∵，

∴

则可列方程组 ，加减消元法

解得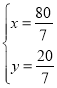

∴四边形的面积为：