Question

【题目】已知：直线AB∥CD，点E. F分别是AB、CD上的点。

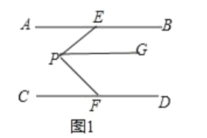
(1)如图1，当点P在AB、CD内部时，试说明：∠EPF=∠AEP+∠CFP；

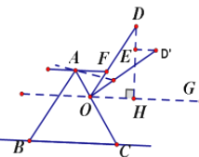
(2)如图2，当点P在AB上方时，∠EPF、∠AEP、∠CFP之间有怎样的数量关系?并说明理由。

Answer 1

【答案】（1）见解析；（2）∠AEP+∠EPF=∠CFP，理由见解析；

【解析】

(1) 证明：过P点作PG∥AB，如图1，

∵PG∥AB，

∴∠EPG=∠AEP，

∵AB∥CD，

∴PG∥CD，

∴∠FPG=∠CFP，

∴∠AEP+∠CFP=∠EPF；

(2)∠AEP+∠EPF=∠CFP，理由如下：

∵∠AEP+∠EPF=∠AGP，

∵CD∥AB，

∴∠APG=∠CFP，

∴∠AEP+∠EPF=∠CFP.