题目内容
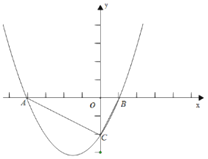
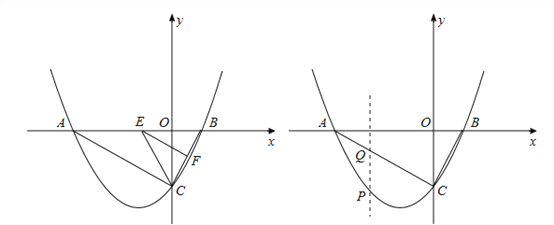
【题目】如图,已知抛物线![]() 轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
(1)求此抛物线的解析式;
(2)设E是线段AB上的动点,作EF∥AC交BC于F,连接CE,当△CEF的面积是△BEF面积的2倍时,求E点的坐标;
(3)若P为抛物线上A、C两点间的一个动点,过P作y轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.
【答案】(1)![]() ;(2)E的坐标是
;(2)E的坐标是![]() ; (3)P点的坐标是(-2,-3).
; (3)P点的坐标是(-2,-3).
【解析】试题分析:(1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数的值;
(2)根据抛物线的解析式可得出C点的坐标,易证得△ABC是直角三角形,则EF⊥BC;△CEF和△BEF同高,则面积比等于底边比,由此可得出CF=2BF;易证得△BEF∽△BAC,根据相似三角形的性质,即可求得BE、AB的比例关系,由此可求出E点坐标;
(3)PQ的长实际是直线AC与抛物线的函数值的差,可设P点横坐标为m,用m表示出P、Q的纵坐标,然后可得出PQ的长与m的函数关系式,根据所得函数的性质即可求出PQ最大时,m的值,也就能求出此时P点的坐标.
试题解析:解:(1)由题意得: 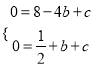 ,解得:
,解得: 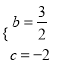 ,∴
,∴![]() ;
;
(2)由(1)知:C(0,﹣2),则AC2=AO2+OC2=20,BC2=BO2+OC2=5.
而AB2=25=AC2+BC2,∴△ACB是直角三角形,且∠ACB=90°,∴AC⊥BC,∵EF∥AC,∴EF⊥BC.∵S△CEF=2S△BEF,∴CF=2BF,BC=3BF.∵EF∥AC,∴ ![]() .
.
∵AB=5,∴BE=![]() ,OE=BE﹣OB=
,OE=BE﹣OB=![]() ,故E(
,故E(![]() ,0);
,0);
(3)设P点坐标为(m, ![]() ).已知A(﹣4,0),C(0,﹣2),设直线AC的解析式为:y=kx﹣2,则有:﹣4k﹣2=0,∴k=﹣
).已知A(﹣4,0),C(0,﹣2),设直线AC的解析式为:y=kx﹣2,则有:﹣4k﹣2=0,∴k=﹣![]() ,∴直线AC的解析式为y=﹣
,∴直线AC的解析式为y=﹣![]() x﹣2,
x﹣2,
∴Q点坐标为(m,﹣ ![]() m﹣2),则PQ=(﹣
m﹣2),则PQ=(﹣![]() m﹣2)﹣(
m﹣2)﹣(![]() )=﹣
)=﹣![]() m2﹣2m=
m2﹣2m=![]() ,∴当m=﹣2,即P(﹣2,﹣3)时,PQ最大,且最大值为2.
,∴当m=﹣2,即P(﹣2,﹣3)时,PQ最大,且最大值为2.
故当P运动到OA垂直平分线上时,PQ的值最大,此时P(﹣2,﹣3).

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
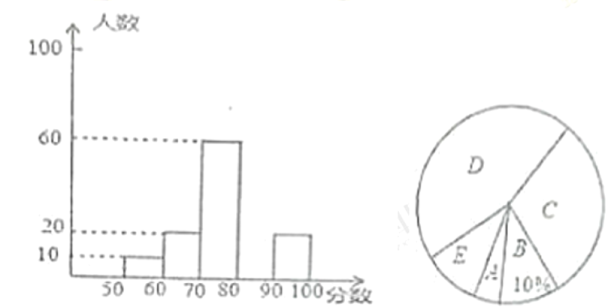
课课通课程标准思维方法与能力训练系列答案【题目】七年级数学研究学习小组在某↑字路口随机调查部分市民对“社会主义核心价值观”的了解情况,统计结果后绘制了如图的两副不完整的统计图,请结合图中相关数据回答下列问题:
得分 | |
|
|
|
|
|
|
|
|
|
|
(1)本次调查的总人数为 人, 在扇形统计图中“心所在扇形的圆心角的度数为 :
(2)补全频数分布图:
(3)若在这周里,该路口共有![]() 人通过,请估计得分超过
人通过,请估计得分超过![]() 的约有多少人?
的约有多少人?