题目内容
如图,梯形ABCD中,AD∥BC,AB=CD=AD=1,∠B=60°,
直线MN是梯形的对称轴,P为直线MN上的一动点,则PC+PD的最小值为()

直线MN是梯形的对称轴,P为直线MN上的一动点,则PC+PD的最小值为()

| A.1 | B. | C. | D.2 |
B
分析:要求PC+PD的最小值,就相当于求BP+PD的最小值,当BPD在同一直线上时,距离最短.
解答:解:连接BP,因为梯形ABCD关于MN对称,
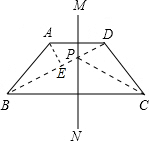
所以,BP=PC,
△ABD是等腰三角形,∠A=120°,
过点A作AE⊥BD于E,在Rt△AEB中,
∠ABE=30°,
∴AE=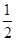 AB=
AB=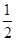 ,
,
由勾股定理得:DE=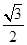
∴BD=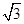
即PC+PD的最小值为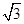 .
.
故选B.
解答:解:连接BP,因为梯形ABCD关于MN对称,

所以,BP=PC,
△ABD是等腰三角形,∠A=120°,
过点A作AE⊥BD于E,在Rt△AEB中,
∠ABE=30°,
∴AE=
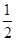 AB=
AB=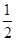 ,
,由勾股定理得:DE=
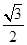
∴BD=
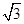
即PC+PD的最小值为
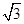 .
.故选B.

练习册系列答案
相关题目



 平分
平分 ;
; ,求
,求 的面积.
的面积.

 中,
中, 平分
平分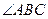 交
交 于点
于点 ,
, 平分
平分
 交
交 于点
于点 .
. ;
; ,则判断四边形
,则判断四边形 是什么特殊四边形,请证明你的结论.
是什么特殊四边形,请证明你的结论. 