题目内容
如图，矩形ABCD中，AB＝4，BC＝8，如果将该矩形沿对角线BD折叠，那么图中阴影部分的面积是 .
10
易得BE=DE，利用勾股定理求得DE的长，利用三角形的面积公式可得阴影部分的面积．
解：根据翻折的性质可知：∠EBD=∠DBC，
又∵AD∥BC，
∴∠ADB=∠DBC，
∴∠ADB=∠EBD，
∴BE=DE，
设BE=DE=x，
∴AE=8-x，
∵四边形ABCD是矩形，
∴∠A=90°，
∴AE2+AB2=BE2，
（8-x）2+42=x2，
x=5，
∴S△EDB=
×5×4=10．
故答案为：10．
解：根据翻折的性质可知：∠EBD=∠DBC，
又∵AD∥BC，
∴∠ADB=∠DBC，
∴∠ADB=∠EBD，
∴BE=DE，
设BE=DE=x，
∴AE=8-x，
∵四边形ABCD是矩形，
∴∠A=90°，
∴AE2+AB2=BE2，
（8-x）2+42=x2，
x=5，
∴S△EDB=
×5×4=10．故答案为：10．
练习册系列答案
相关题目
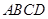的外侧作等边
，则
的度数为（ ）
、
、
分别是等边
的边BC、CA、AB的中点，在图2中，
、
、
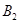分别是
的边
、
、
的中点，……，按此规律，则第n个图形中菱形的个数共有（ ）个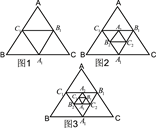
B. 
C. 
D. 
，若
，
，则梯形ABCD的周长为____▲_____。
折叠后，点
分别落在
的位置．若
，则
等于_______度．