题目内容
【题目】已知正方形ABCD中，AB＝6，点P是射线BC上的一动点，过点P作PE⊥PA交直线CD于E，连AE．
（1）如图1，若BP＝2，求DE的长；
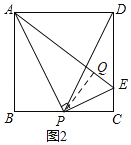
（2）如图2，若AP平分∠BAE，连PD，求tan∠DPE的值；
（3）直线PD，AE交于点F，若BC＝4PC，则
＝ ．
【答案】（1）
；（2）
；（3）
或
【解析】
（1）证明△ABP∽△PCE，可以解决问题；
（2）如图2，过P作PQ⊥AE于Q，根据角平分线的性质得BP＝PQ＝PC＝3，根据△ABP∽△PCE，得CE＝1，DE＝5，根据对角互补的四边形是圆内接四边形，得∠DAE＝∠DPE，由等角的三角函数可得结论；
（3）分两种情况：①当P在线段BC上时，如图3，过E作EG∥PC，交PD于G，
②当P在射线BC上时，过E作EQ∥AD，交DF于Q；证明两三角形相似，列比例式可得结论．
解：（1）如图1，∵四边形ABCD是正方形，
∴AB＝CD＝BC＝AD＝6，∠B＝∠C＝∠D＝90°，
∵BP＝2，
∴PC＝4，
∵AP⊥PE，
∴∠APE＝∠APB+∠CPE＝90°，
∵∠APB+∠BAP＝90°，
∴∠BAP＝∠CPE，
∴△ABP∽△PCE，
∴
，即
∴CE＝
，
∴DE＝CD﹣CE＝6﹣＝；
（2）如图2，过P作PQ⊥AE于Q，
∵AP平分∠BAE，∠B＝90°，
∴BP＝PQ，
∵∠APE＝∠B＝90°，∠BAP＝∠PAE，
∴∠APB＝∠AEP＝∠PEC，
∵∠C＝90°，
∴PC＝PQ＝BP＝
BC＝3，
由（1）得：△ABP∽△PCE，
∴，即
∴CE＝1，
∴DE＝CD﹣CE＝5，
∵∠ADC+∠APE＝180°，
∴A、D、E、P四点共圆，
∴∠DAE＝∠DPE，
∴tan∠DPE＝tan∠DAE＝
；
（3）分两种情况：
①当P在线段BC上时，如图3，过E作EG∥PC，交PD于G，
∵BC＝4PC，BC＝6，
∴BP＝
，PC＝
，
由（1）知：DE＝，
∵EG∥PC，
∴△DGE∽△DPC，
∴
，即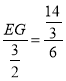
，
∴EG＝
，
∵AD∥PC，
∴AD∥EG，
∴△AFD∽△EFG，
∴
＝；
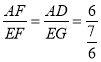②当P在射线BC上时，如图4，
∵BC＝4PC，BC＝6，
∴PC＝，
∴BP＝BC+CP＝
，
∵∠APB+∠BPE＝∠BPE+∠CEP＝90°，
∴∠APB＝∠CEP，
∴∠B＝∠ECP＝90°，
∴△ABP∽△PCE，
∴
，即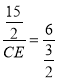
∴CE＝
，
过E作EQ∥AD，交DF于Q，
∵EQ∥CP，
∴△DCP∽△DEQ，
∴
，即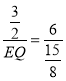
∴EQ＝
，
∵EQ∥AD，
∴△EQF∽△ADF，
∴
．
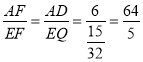综上所述，则
＝或；
故答案为：或．
