题目内容
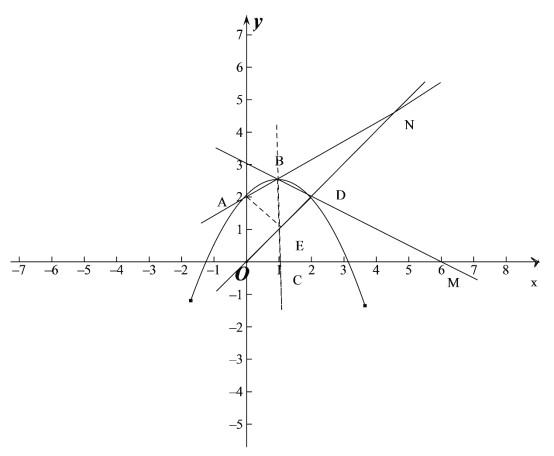
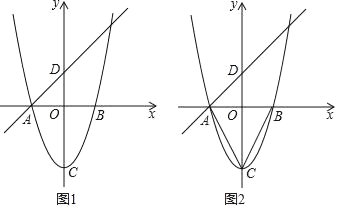
【题目】已知开口向下的抛物线y=ax2-2ax+2与y轴的交点为A，顶点为B，对称轴与x轴的交点为C，点A与点D关于对称轴对称，直线BD与x轴交于点M，直线AB与直线OD交于点N．
(1)求点D的坐标.
(2)求点M的坐标(用含a的代数式表示).
(3)当点N在第一象限，且∠OMB=∠ONA时，求a的值．
【答案】（1）D（2,2）；（2）
；（3）
【解析】
(1)令x=0求出A的坐标，根据顶点坐标公式或配方法求出顶点B的坐标、对称轴直线，根据点A与点D关于对称轴对称，确定D点坐标.
(2)根据点B、D的坐标用待定系数法求出直线BD的解析式，令y=0，即可求得M点的坐标.
（3）根据点A、B的坐标用待定系数法求出直线AB的解析式，求直线OD的解析式，进而求出交点N的坐标，得到ON的长.过A点作AE⊥OD，可证△AOE为等腰直角三角形，根据OA=2，可求得AE、OE的长，表示出EN的长.根据tan∠OMB=tan∠ONA，得到比例式，代入数值即可求得a的值.
（1）当x=0时，
，
∴A点的坐标为（0,2）
∵
∴顶点B的坐标为：（1,2-a），对称轴为x= 1，
∵点A与点D关于对称轴对称
∴D点的坐标为：（2，2）
（2）设直线BD的解析式为：y=kx+b
把B（1,2-a）D（2，2）代入得：
，解得：
∴直线BD的解析式为：y=ax+2-2a
当y=0时，ax+2-2a=0，解得：x=
∴M点的坐标为：
（3）由D(2，2)可得：直线OD解析式为：y=x
设直线AB的解析式为y=mx+n,代入A(0，2)B（1,2-a）可得：
解得：
∴直线AB的解析式为y= -ax+2
联立成方程组：
，解得：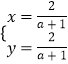
∴N点的坐标为：（
）
ON=
（
）
过A点作AE⊥OD于E点，则△AOE为等腰直角三角形.
∵OA=2
∴OE=AE=，EN=ON-OE=（）-=
)
∵M，C(1,0)， B（1,2-a）
∴MC=
，BE=2-a
∵∠OMB=∠ONA
∴tan∠OMB=tan∠ONA
∴
，即
解得：a=
或
∵抛物线开口向下，故a<0，
∴ a=舍去，
