题目内容
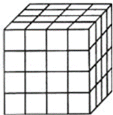
【题目】如图,把一个木制正方体的表面涂上颜色,然后将正方体分割成64个大小相同的小正方体.从这些小正方体中任意取出一个,求取出的小正方体:
(1)三面涂有颜色的概率;
(2)两面涂有颜色的概率;
(3)各个面都没有颜色的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)三面涂有颜色的小正方体是在8个顶点处,共8个,再根据概率公式解答即可;
(2)两面涂有颜色的小正方体是在12条棱的中间处,共24个,再根据概率公式解答即可;
(3)各个面都没有颜色的小正方体是在6个面的中间处,共8个,再根据概率公式解答即可.
解:(1)因为三面涂有颜色的小正方体有8个,
所以P(三面涂有颜色)=![]() ;
;
(2)因为两面涂有颜色的小正方体有24个,
所以P(两面涂有颜色)=![]() ;
;
(3)因为各个面都没有涂颜色的小正方体共有8个,
所以P(各个面都没有涂颜色)=![]() .
.

练习册系列答案
相关题目